(本題滿分14分)本題共有2個小題,每小題滿分各7分.
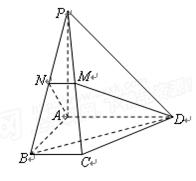
如圖,在四棱錐

中,底面為直角梯形,

,

垂直于底面

,

,

分別為
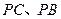
的中點.
(1)求證:

;
(2)求

與平面

所成的角.
解法一:(1)以

點為坐標原點建立空間直角坐標系
(圖略),由

得

,

,

,
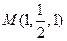

(2分)
因為

(5分) 所以

. (7分)
(2)因為


,所以

,又

,
故

平面

,即
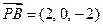
是平面

的法向量.(

9分)
設

與平面

所成的角為

,又

,設

與

夾角為

,
則

, (12分)
又

,故


,故

與平面

所成的角是

. (14分)
解法二:(1)證明:因為

是

的中點,

, 所以

(2分)
由

底面

,得

,又

,即

,


平面

,

(4

分)

面

,

(7分)
(2)聯(lián)結

,

平面

,故

為

與面

所成角(9分)

在

中,

,
在

中,
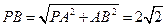
,故

,
在
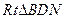
中,

,又

, (12分)
故

與平面

所成的角是

(14分)
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,正三棱錐

的三條側棱
、

、

兩兩垂直,且長度均為2.

、

分別是
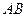
、
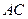
的中點,

是

的中點,過

的平面與側棱
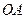
、

、

或其延長線分別相交于

、

、

,已知

.
(1)求證:

⊥面
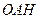
;
(2)求二面角

的大小.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知一個四棱錐P—ABCD的三視圖(正視圖與側視圖為直角三角形,俯視圖是帶有一條對角形的正方形)如下,E是側棱PC上的動點。
(1)求四棱錐P—ABCD的體積;
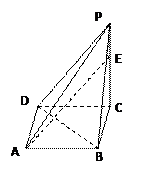
(2)是否不論點E 在何位置都有BD⊥AE,證明你的結論。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題

、

、

是表面積為

的球面上三點,

,

,

,

為球心,則直線

與截面

所成的角是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,正方形DEMF內(nèi)接于△ABC,若

,
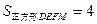
,求


查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
畫出下列物體的三視圖.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題

如圖所示,某幾何體的正視圖、側視圖均為半圓和等邊三角形的
組合,俯視圖為圓形,則該幾何體的全面積為

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知某幾何體的三視

圖如右,根據(jù)圖中標出的尺寸


(單位:cm),可得這個幾何體的體積是


(

)學
查看答案和解析>>

 中,底面為直角梯形,
中,底面為直角梯形, ,
, 垂直于底面
垂直于底面 ,
, ,
, 分別為
分別為 的中點.
的中點.  ;
; 與平面
與平面 所成的角.
所成的角.
 的三條側棱
的三條側棱 、
、 、
、 兩兩垂直,且長度均為2.
兩兩垂直,且長度均為2. 、
、 分別是
分別是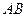 、
、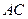 的中點,
的中點, 是
是 的中點,過
的中點,過 的平面與側棱
的平面與側棱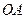 、
、 、
、 或其延長線分別相交于
或其延長線分別相交于 、
、 、
、 ,已知
,已知 .
. ⊥面
⊥面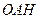 ;
; 的大小.
的大小.
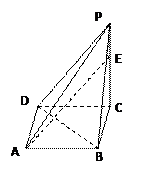 (2)是否不論點E 在何位置都有BD⊥AE,證明你的結論。
(2)是否不論點E 在何位置都有BD⊥AE,證明你的結論。