
【題目】在如圖所示的四棱錐![]() 中,四邊形
中,四邊形![]() 為正方形,
為正方形,![]() ,
,![]() 平面
平面![]() ,且
,且![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 的中點,
的中點,![]() .
.
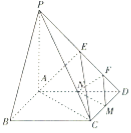
⑴證明:![]() 平面
平面![]() ;
;
⑵若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】⑴證明見解析;⑵![]() .
.
【解析】
試題分析:⑴做輔助線,由![]() 為
為![]() 中點,
中點,![]() 為
為![]() 中點
中點![]()
![]() .又
.又![]()
![]()
![]() 為
為![]() 中點,又
中點,又![]() ,
,![]()
![]()
![]() 為
為![]() 中點
中點![]()
![]()
![]()
![]()
![]()
![]() 平面
平面![]() ;⑵由
;⑵由![]() 平面
平面![]()
![]()
![]() ,又
,又![]()
![]()
![]() 平面
平面![]() .以
.以![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標系,求出平面
軸建立空間直角坐標系,求出平面![]() 的一個法向量
的一個法向量![]() ,平面
,平面![]() 的法向量為
的法向量為![]()
![]()
![]() . 由圖可知,二面角
. 由圖可知,二面角![]() 為鈍角
為鈍角![]() 二面角
二面角![]() 的余弦值為
的余弦值為![]() .
.
試題解析:⑴證明:連結![]() ,分別交
,分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,連結
,連結![]() 、
、![]() ,
,
∵![]() 為
為![]() 中點,
中點,![]() 為
為![]() 中點,∴
中點,∴![]() .……………………2分
.……………………2分
又![]() ,∴
,∴![]() 為
為![]() 中點,又
中點,又![]() ,
,![]() ,∴
,∴![]() 為
為![]() 中點,
中點,
∴![]() ,∴
,∴![]() .……………………………………4分
.……………………………………4分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .………………………………5分
.………………………………5分
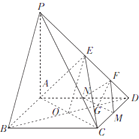
⑵解:∵![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .……………………………………6分
.……………………………………6分
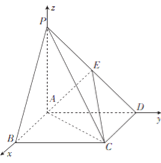
如圖 ,以![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
則![]() ,
,
則![]() ,
,![]() ,………………………………7分
,………………………………7分
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一個法向量
的一個法向量![]() .…………8分
.…………8分
設平面![]() 的法向量為
的法向量為![]() ,
,
則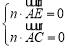 ,即
,即![]() ,…………………………9分
,…………………………9分
令![]() ,則
,則![]() ,
,![]() ,∴
,∴![]() ,…………10分
,…………10分
∴![]() .……………………………………11分
.……………………………………11分
由圖可知,二面角![]() 為鈍角,
為鈍角,
∴二面角![]() 的余弦值為
的余弦值為![]() .……………………………………12分
.……………………………………12分


科目:高中數學 來源: 題型:
【題目】某地區2008年至2014年中,每年的居民人均純收入y(單位:千元)的數據如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
對變量t與y進行相關性檢驗,得知t與y之間具有線性相關關系.
(1)求y關于t的線性回歸方程;
(2)預測該地區2017年的居民人均純收入.
附:回歸直線的斜率和截距的最小二乘估計公式分別為:
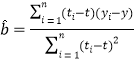 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的二次函數f(x)=x2+(2t-1)x+1-2t.
(1)求證:對于任意t∈R,方程f(x)=1必有實數根;
(2)若![]() <t<
<t<![]() ,求證:方程f(x)=0在區間(-1,0)及
,求證:方程f(x)=0在區間(-1,0)及![]() 內各有一個實數根.
內各有一個實數根.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩家商場對同一種商品展開促銷活動,對購買該商品的顧客兩家商場的獎勵方案如下:
甲商場:顧客轉動如圖所示轉盤,當指針指向陰影部分(圖中兩個陰影部分均為扇形,且每個扇形圓心角均為![]() ,邊界忽略不計)即為中獎.
,邊界忽略不計)即為中獎.
乙商場:從裝有4個白球,4個紅球和4個籃球的盒子中一次性摸出3球(這些球初顏色外完全相同),如果摸到的是3個不同顏色的球,即為中獎.

(Ⅰ)試問:購買該商品的顧客在哪家商場中獎的可能性大?說明理由;
(Ⅱ)記在乙商場購買該商品的顧客摸到籃球的個數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】閱讀:
已知![]() 、
、![]() ,
,![]() ,求
,求![]() 的最小值.
的最小值.
解法如下:![]() ,
,
當且僅當![]() ,即
,即![]() 時取到等號,
時取到等號,
則![]() 的最小值為
的最小值為![]() .
.
應用上述解法,求解下列問題:
(1)已知![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(2)已知![]() ,求函數
,求函數![]() 的最小值;
的最小值;
(3)已知正數![]() 、
、![]() 、
、![]() ,
,![]() ,
,
求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,集合A={x|-5<x<5},B={x|0≤x<7},求:(1)A∩B;(2)A∪B;(3)A∪(UB);(4)B∩(UA);(5)(UA)∩(UB).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市居民自來水收費標準如下:每戶每月用水不超過5噸時,每噸為![]() 元,當用水超過5噸時,超過部分每噸4元。某月甲、乙兩戶共交水費
元,當用水超過5噸時,超過部分每噸4元。某月甲、乙兩戶共交水費![]() 元,已知甲、乙兩戶該月用水量分別為
元,已知甲、乙兩戶該月用水量分別為![]() 噸。
噸。
(1)求![]() 關于
關于![]() 的函數。
的函數。
(2)若甲、乙兩戶該月共交水費![]() 元,分別求甲、乙兩戶該月的用水量和水費。
元,分別求甲、乙兩戶該月的用水量和水費。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種電子儀器的固定成本為20 000元,每生產一臺儀器需要增加投入100元,已知總收益滿足函數:R(x)=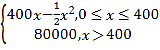 其中x是儀器的月產量.當月產量為何值時,公司所獲得利潤最大?最大利潤是多少?
其中x是儀器的月產量.當月產量為何值時,公司所獲得利潤最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com