
【題目】已知正三棱柱![]() 中,
中,![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
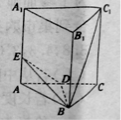
(Ⅰ)當![]() 時,求證
時,求證![]() ;
;
(Ⅱ)是否存在點![]() ,使二面角
,使二面角![]() 等于60°?若存在,求
等于60°?若存在,求![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
【答案】(Ⅰ)證明見解析;(Ⅱ)存在點![]() ,當
,當![]() 時,二面角
時,二面角![]() 等于
等于![]() .
.
【解析】
試題分析:(Ⅰ)證明:連接![]() ,
,![]() 由
由![]() 為正三棱柱
為正三棱柱![]()
![]() 為正三角形
為正三角形![]()
![]() ,
,
又平面![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
![]()
![]() .易得
.易得![]()
![]()
![]() 丄平面
丄平面![]()
![]()
![]() .(Ⅱ)假設存在點
.(Ⅱ)假設存在點![]() 滿足條件,設
滿足條件,設![]() .由
.由![]() 丄平面
丄平面![]()
![]() ,建立空間直角坐標系
,建立空間直角坐標系![]() ,求得平面
,求得平面![]() 的一個法向量為
的一個法向量為
![]() ,平面
,平面![]() 的一個法向量為
的一個法向量為![]()
![]()
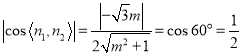
![]()
![]() .
.
試題解析:(Ⅰ)證明:連接![]() ,
,
因為![]() 為正三棱柱,所以
為正三棱柱,所以![]() 為正三角形,
為正三角形,
又因為![]() 為
為![]() 的中點,所以
的中點,所以![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .
.
因為![]() ,所以
,所以![]() ,
,
所以在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,所以
,所以![]() ,即
,即![]() .
.
又![]() ,
,
所以![]() 丄平面
丄平面![]() ,
,![]() 面
面![]() ,所以
,所以![]() .
.
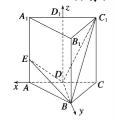
(Ⅱ)假設存在點![]() 滿足條件,設
滿足條件,設![]() .
.
取![]() 的中點
的中點![]() ,連接
,連接![]() ,則
,則![]() 丄平面
丄平面![]() ,
,
所以![]() ,
,
分別以![]() 所在直線為
所在直線為![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,
,
則![]() ,
,
所以![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則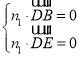 ,
,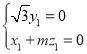 令
令![]() ,得
,得![]() ,
,
同理,平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則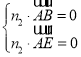 ,
,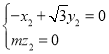 取
取![]() ,
,
∴![]() .
.
∴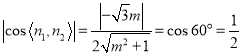 ,解得
,解得![]() ,
,
故存在點![]() ,當
,當![]() 時,二面角
時,二面角![]() 等于
等于![]() .
.


科目:高中數學 來源: 題型:
【題目】國慶期間,某旅行社組團去風景區旅游,若旅行團人數在 ![]() 人或
人或 ![]() 人以下,每人需交費用為
人以下,每人需交費用為 ![]() 元;若旅行團人數多于
元;若旅行團人數多于 ![]() 人,則給予優惠:每多
人,則給予優惠:每多 ![]() 人,人均費用減少
人,人均費用減少 ![]() 元,直到達到規定人數
元,直到達到規定人數 ![]() 人為止.旅行社需支付各種費用共計
人為止.旅行社需支付各種費用共計 ![]() 元.
元.
Ⅰ 寫出每人需交費用 ![]() 關于人數
關于人數 ![]() 的函數;
的函數;
Ⅱ 旅行團人數為多少時,旅行社可獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一次函數f(x)為增函數,且f(f(x))=4x+9,g(x)=mx+m+3(m∈R).
(1)當x∈[-1,2]時,若不等式g(x)>0恒成立,求m的取值范圍;
(2)如果函數F(x)=f(x)g(x)為偶函數,求m的值;
(3)當函數f(x)和g(x)滿足f(g(x))=g(f(x))時,求函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的左,右頂點分別為
的左,右頂點分別為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 軸垂直,
軸垂直,![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的動點,且滿足
兩側的動點,且滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了參加師大附中第30界田徑運動會的開幕式,高三年級某6個班聯合到集市購買了6根竹竿,作為班旗的旗桿之用,它們的長度分別為3.8,4.3,3.6,4.5,4.0,4.1(單位:米).
(Ⅰ)若從中隨機抽取兩根竹竿,求長度之差不超過0.5米的概率;
(Ⅱ)若長度不小于4米的竹竿價格為每根10元,長度小于4米的竹竿價格為每根![]() 元.從這6根竹竿中隨機抽取兩根,若期望這兩根竹竿的價格之和為18元,求
元.從這6根竹竿中隨機抽取兩根,若期望這兩根竹竿的價格之和為18元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com