
【題目】已知函數f(x)= ![]() 在點(1,f(1))處的切線方程為x+y=2. (Ⅰ)求a,b的值;
在點(1,f(1))處的切線方程為x+y=2. (Ⅰ)求a,b的值;
(Ⅱ)若對函數f(x)定義域內的任一個實數x,都有xf(x)<m恒成立,求實數m的取值范圍.
(Ⅲ) 求證:對一切x∈(0,+∞),都有3﹣(x+1)f(x)> ![]() ﹣
﹣ ![]() 成立.
成立.
【答案】解:(Ⅰ)f′(x)= 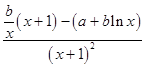 , 而點(1,f(1))在直線x+y=2上,∴f(1)=1,
, 而點(1,f(1))在直線x+y=2上,∴f(1)=1,
又直線x+y=2的斜率為﹣1,∴f′(1)=﹣1,
故有 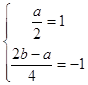 ,解得:
,解得: ![]() ;
;
(Ⅱ)由(Ⅰ)得f(x)= ![]() (x>0),由xf(x)<m,得:
(x>0),由xf(x)<m,得: ![]() <m,
<m,
令g(x)= ![]() ,g′(x)=
,g′(x)= ![]() ,
,
令h(x)=1﹣x﹣lnx,則h′(x)=﹣1﹣ ![]() <0,(x>0),
<0,(x>0),
∴h(x)在區間(0,+∞)上是減函數,
∴當0<x<1時,h(x)>h(1)=0,當x>1時,h(x)<h(1)=0,
從而當0<x<1時,g′(x)>0,當x>1時,g′(x)<0,
∴g(x)在(0,1)是增函數,在(1,+∞)是減函數,
故g(x)max=g(1)=1,
要使 ![]() <m成立,只需m>1,故m的取值范圍是(1,+∞);
<m成立,只需m>1,故m的取值范圍是(1,+∞);
(Ⅲ)證明:要證3﹣(x+1)f(x)=lnx+1> ![]() ﹣
﹣ ![]() ,對x>0成立,
,對x>0成立,
即證明:xlnx+x> ![]() ﹣
﹣ ![]() 對x>0成立,
對x>0成立,
設φ(x)=xlnx+x(x>0),φ′(x)=lnx+2,
當x>e﹣2時,φ′(x)>0,φ(x)遞增;當0<x<e﹣2時,φ′(x)<0,φ(x)遞減;
∴φ(x)min=φ(e﹣2)=﹣ ![]() ,
,
設g(x)= ![]() ﹣
﹣ ![]() (x>0),g′(x)=
(x>0),g′(x)= ![]() ,
,
當0<x<1時,g′(x)>0,g(x)遞增;當x>1時,g′(x)<0,g(x)遞減;
∴g(x)max=g(1)=﹣ ![]() ,∴φ(x)min=﹣
,∴φ(x)min=﹣ ![]() >g(x)max=﹣
>g(x)max=﹣ ![]() ,
,
∴xlnx+x> ![]() ﹣
﹣ ![]() ,對x>0成立,
,對x>0成立,
∴3﹣(x+1)f(x)=lnx+1> ![]() ﹣
﹣ ![]() 對x>0成立
對x>0成立
【解析】(Ⅰ)求出函數的導數,計算f(1),f′(1),得到關于a,b的方程組,解出即可;(Ⅱ)問題轉化為 ![]() <m,令g(x)=
<m,令g(x)= ![]() ,根據函數的單調性求出g(x)的最大值,從而求出a的范圍即可;(Ⅲ)問題轉化為證明:xlnx+x>
,根據函數的單調性求出g(x)的最大值,從而求出a的范圍即可;(Ⅲ)問題轉化為證明:xlnx+x> ![]() ﹣
﹣ ![]() 對x>0成立,設φ(x)=xlnx+x(x>0),g(x)=
對x>0成立,設φ(x)=xlnx+x(x>0),g(x)= ![]() ﹣
﹣ ![]() (x>0),根據函數的單調性分別求出φ(x)的最小值和g(x)的最大值即可.
(x>0),根據函數的單調性分別求出φ(x)的最小值和g(x)的最大值即可.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】已知正項數列{an}的前n項和為Sn , 且a1=1,an+12=Sn+1+Sn .
(1)求{an}的通項公式;
(2)設bn=a2n﹣1![]() , 求數列{bn}的前n項和Tn .
, 求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在我國古代著名的數學專著《九章算術》里有一段敘述:今有良馬與駑馬發長安至齊,齊去長安一千一百二十五里,良馬初日行一百零三里,日增十三里;駑馬初日行九十七里,日減半里;良馬先至齊,復還迎駑馬,二馬相逢.問:幾日相逢?( )
A.9日
B.8日
C.16日
D.12日
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|cosx|sinx,給出下列五個說法: ①f( ![]() π)=﹣
π)=﹣ ![]() ;
;
②若|f(x1)|=|f(x2)|,則x1=x2+kπ(k∈Z);
③f(x)在區間[﹣ ![]() ,
, ![]() ]上單調遞增;
]上單調遞增;
④函數f(x)的周期為π.
⑤f(x)的圖象關于點( ![]() ,0)成中心對稱.
,0)成中心對稱.
其中正確說法的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在(﹣π,0)∪(0,π)的奇函數,其導函數為f'(x),且 ![]() ,當x∈(0,π)時,f'(x)sinx﹣f(x)cosx<0,則關于x的不等式
,當x∈(0,π)時,f'(x)sinx﹣f(x)cosx<0,則關于x的不等式 ![]() 的解集為( )
的解集為( )
A.![]()
B.![]() ??
??
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等腰△ABC中,AC=BC= ![]() ,AB=2,E、F分別為AC、BC的中點,將△EFC沿EF折起,使得C到P,得到四棱錐P﹣ABFE,且AP=BP=
,AB=2,E、F分別為AC、BC的中點,將△EFC沿EF折起,使得C到P,得到四棱錐P﹣ABFE,且AP=BP= ![]() .
. 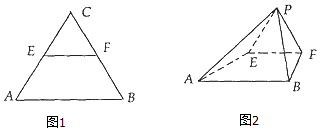
(1)求證:平面EFP⊥平面ABFE;
(2)求二面角B﹣AP﹣E的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=f(x)導函數的圖象如圖所示,則下列說法錯誤的是( )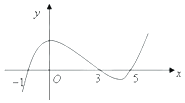
A.(﹣1,3)為函數y=f(x)的遞增區間
B.(3,5)為函數y=f(x)的遞減區間
C.函數y=f(x)在x=0處取得極大值
D.函數y=f(x)在x=5處取得極小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x|+|x+1|.
(1)若x∈R,恒有f(x)≥λ成立,求實數λ的取值范圍;
(2)若m∈R,使得m2+2m+f(t)=0成立,試求實數t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com