已知
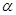
、
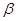
是不同的兩個平面,直線
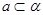
,直線

,命題
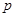
:
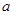
與
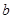
無公共點;命題
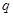
:
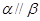
, 則
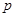
是
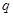
的
條件.
試題分析:已知
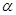
、
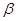
是不同的兩個平面,直線
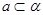
,直線

,
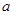
與
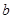
無公共點,無法推出
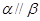
;而
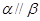
可推出
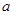
與
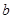
無公共點,所以
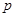
是
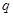
的必要非充分條件.
點評:基礎(chǔ)題,充要條件的判斷問題,是高考不可少的內(nèi)容,特別是充要條件可以和任何知識點相結(jié)合。充要條件的判斷一般有三種思路:定義法、等價關(guān)系轉(zhuǎn)化法、集合關(guān)系法。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(12分)已知
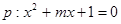
有兩個不等的負(fù)根,
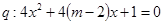
無實數(shù)根,若p或q為真,p且q為假,求m的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
有下面四個判斷:
①命題:“設(shè)
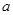
、
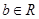
,若
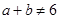
,則
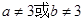
”是一個假命題
②若“
p或
q”為真命題,則
p、
q均為真命題
③命題“
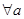
、

”的否定是:
“

、
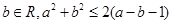
”
④若函數(shù)
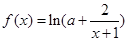
的圖象關(guān)于原點對稱,則
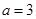
其中正確的個數(shù)共有( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
給出下列四個命題:
①若集合
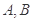
滿足
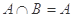
則
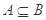
;
②給定命題
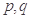
,若
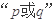
為真,則
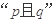
為真;
③設(shè)
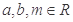
,若
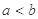
,則
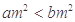
;
④若直線
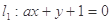
與直線
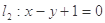
垂直,則
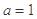
.
其中正確命題的個數(shù)是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
給出下列命題:
(1)命題“若b
2-4ac<0,則方程ax
2+bx+c=0(a≠0)無實根”的否命題
(2)命題“△ABC中,AB=BC=CA,那么△ABC為等邊三角形”的逆命題
(3)命題“若a>b>0,則
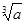
>
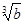
>0”的逆否命題
(4)“若m>1,則mx
2-2(m+1)x+(m-3)>0的解集為R”的逆命題
其中真命題的序號為__________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
若
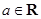
,則“
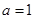
”是“
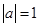
”的( )條件( )
| A.充分而不必要 | B.必要而不充分 | C.充要 | D.既不充分也不必要 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
命題“存在
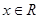
,使得
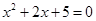
”的否定是
.
查看答案和解析>>

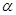 、
、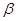 是不同的兩個平面,直線
是不同的兩個平面,直線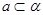 ,直線
,直線 ,命題
,命題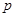 :
: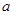 與
與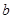 無公共點;命題
無公共點;命題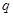 :
: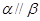 , 則
, 則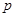 是
是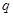 的 條件.
的 條件.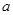 、
、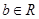 ,若
,若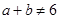 ,則
,則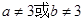 ”是一個假命題
”是一個假命題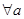 、
、 ”的否定是:
”的否定是: 、
、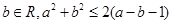 ”
”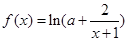 的圖象關(guān)于原點對稱,則
的圖象關(guān)于原點對稱,則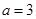
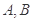 滿足
滿足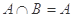 則
則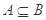 ;
;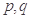 ,若
,若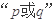 為真,則
為真,則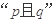 為真;
為真;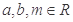 ,若
,若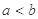 ,則
,則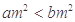 ;
;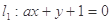 與直線
與直線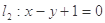 垂直,則
垂直,則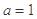 .
.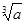 >
>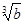 >0”的逆否命題
>0”的逆否命題