本題利用純代數討論是很繁瑣的,要用數形結合.原不等式x
2<2-|x-t|,即|x-t|<2-x
2,分別畫出函數y
1=|x-t|,y
2=2-x
2,這個很明確,是一個開口向下,關于y軸對稱,最大值為2的拋物線;要存在x<0使不等式|x-t|<2-x
2成立,則y
1的圖象應該在第二象限(x<0)和y
2的圖象有交點,再分兩種臨界講座情況,當t≤0時,y
1的右半部分和y
2在第二象限相切;當t>0時,要使y
1和y
2在第二象限有交點,最后綜上得出實數t的取值范圍.
解:不等式x
2<2-|x-t|,即|x-t|<2-x
2,
令y
1=|x-t|,y
1的圖象是關于x=t對稱的一個V字形圖形,其象位于第一、二象限;
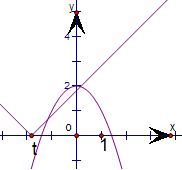
y
2=2-x
2,是一個開口向下,關于y軸對稱,最大值為2的拋物線;
要存在x<0,使不等式|x-t|<2-x
2成立,則y
1的圖象應該在第二象限和y
2的圖象有交點,兩種臨界情況,①當t≤0時,y
1的右半部分和y
2在第二象限相切:
y
1的右半部分即y
1=x-t,
聯列方程y=x-t,y=2-x
2,只有一個解;
即x-t=2-x
2,即x
2+x-t-2=0,△=1+4t+8=0,得:t=-

;
此時y
1恒大于等于y
2,所以t=-

取不到;
所以-

<t≤0;
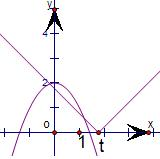
②當t>0時,要使y
1和y
2在第二象限有交點,
即y
1的左半部分和y
2的交點的位于第二象限;
無需聯列方程,只要y
1與y軸的交點小于2即可;
y
1=t-x與y軸的交點為(0,t),所以t<2,
又因為t>0,所以0<t<2;
綜上,實數t的取值范圍是:-

<t<2;
故答案為:(-

,2).

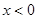 使得不等式
使得不等式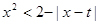 成立,則實數t的取值范圍是 。
成立,則實數t的取值范圍是 。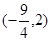


 ;
; 取不到;
取不到; <t≤0;
<t≤0; <t<2;
<t<2; ,2).
,2).

 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案