
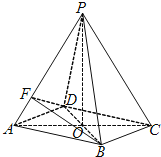
【題目】如圖所示,在四棱錐![]() 中,底面四邊形ABCD是菱形,
中,底面四邊形ABCD是菱形, ![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形, ![]() ,
, ![]() .
.
![]() Ⅰ
Ⅰ![]() 求證:
求證: ![]() 底面ABCD;
底面ABCD;
![]() Ⅱ
Ⅱ![]() 求直線CP與平面BDF所成角的大小;
求直線CP與平面BDF所成角的大小;
![]() Ⅲ
Ⅲ![]() 在線段PB上是否存在一點M,使得
在線段PB上是否存在一點M,使得![]() 平面BDF?如果存在,求
平面BDF?如果存在,求![]() 的值,如果不存在,請說明理由.
的值,如果不存在,請說明理由.
【答案】![]() Ⅰ
Ⅰ![]() 見解析;
見解析; ![]() Ⅱ
Ⅱ![]() Ⅲ
Ⅲ![]() .
.
【解析】試題分析:
(Ⅰ) 由題意可得![]() ,從而可得
,從而可得![]() 底面ABCD. (Ⅱ)建立空間直角坐標系,利用坐標法求解即可得到所求的線面角.
底面ABCD. (Ⅱ)建立空間直角坐標系,利用坐標法求解即可得到所求的線面角. ![]() Ⅲ
Ⅲ![]() 根據坐標法求解探索性問題,假設存在點M滿足條件,并設且
根據坐標法求解探索性問題,假設存在點M滿足條件,并設且![]() ,求得點點M坐標后,根據
,求得點點M坐標后,根據![]() 與平面BDF的法向量垂直可得
與平面BDF的法向量垂直可得![]() ,從而得到符合題意的點M存在.
,從而得到符合題意的點M存在.
試題解析:
![]() Ⅰ
Ⅰ![]() 證明:∵四邊形ABCD是菱形,
證明:∵四邊形ABCD是菱形,
∴O為![]() 中點
中點![]()
又![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 底面
底面![]()
![]() Ⅱ
Ⅱ![]() 解:由底面ABCD是菱形可得
解:由底面ABCD是菱形可得![]() ,又由
,又由![]() Ⅰ
Ⅰ![]() 可知
可知![]() .
.
建立如圖所示的空間直角坐標系![]() .
.

由![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形, ![]() ,可得
,可得![]() .
.
所以![]()
∴![]()
![]() .
.
由已知可得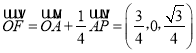 ,
,
設平面BDF的法向量為![]() ,
,
由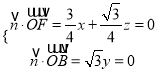 ,可得
,可得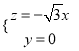 ,
,
令![]() ,則
,則![]() .
.
設直線CP與平面BDF所成的角為![]() ,
,
則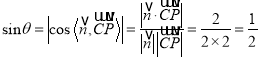 ,
,
又![]() ,
,
∴![]() .
.
∴直線CP與平面BDF所成角的大小為![]() .
.
![]() Ⅲ
Ⅲ![]() 解:假設存在點M滿足條件,且
解:假設存在點M滿足條件,且![]() ,
,
則![]() .
.
若使![]() 平面BDF,需且僅需
平面BDF,需且僅需![]() 且
且![]()
![]() 平面BDF,
平面BDF,
由![]() ,解得
,解得![]() 符合題意.
符合題意.
∴在線段PB上存在一點M,使得![]() 平面BDF,且
平面BDF,且![]()


科目:高中數學 來源: 題型:
【題目】如圖,△ABC是直角三角形,∠ABC=90°,以AB為直徑的圓O交AC于點E,點D是BC邊的中點,連接OD交圓O于點M. 
(1)求證:O、B、D、E四點共圓;
(2)求證:2DE2=DMAC+DMAB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校課題組為了研究學生的數學成績和物理成績之間的關系,隨機抽取高二年級20名學生某次考試成績(百分制)如表所示:
序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
數學成績 | 95 | 75 | 80 | 94 | 92 | 65 | 67 | 84 | 98 | 71 | 67 | 93 | 64 | 78 | 77 | 90 | 57 | 83 | 72 | 83 |
物理成績 | 90 | 63 | 72 | 87 | 91 | 71 | 58 | 82 | 93 | 81 | 77 | 82 | 48 | 85 | 69 | 91 | 61 | 84 | 78 | 86 |
若數學成績90分(含90分)以上為優秀,物理成績85(含85分)以上為優秀.有多少把握認為學生的數學成績與物理成績之間有關系( )
A.99.5%
B.99.9%
C.97.5%
D.95%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,點E、F分別是AB、CD的中點,點G在EF上,沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF,如圖2.
(1)當AG+GC最小時,求證:BD⊥CG;
(2)當2VB﹣ADGE=VD﹣GBCF時,求二面角D﹣BG﹣C平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)滿足對任意的m,n都有f(m+n)=f(m)+f(n)-1,設g(x)=f(x)+![]() (a>0,a≠1),g(ln2018)=-2015,則g(ln
(a>0,a≠1),g(ln2018)=-2015,則g(ln![]() )=______.
)=______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,直角梯形
,直角梯形![]() 通過直角梯形
通過直角梯形![]() 以直線
以直線![]() 為軸旋轉得到,且使得平面
為軸旋轉得到,且使得平面![]() 平面
平面![]() .
. ![]() 為線段
為線段![]() 的中點,
的中點, ![]() 為線段
為線段![]() 上的動點.
上的動點.

(![]() )求證:
)求證: ![]() .
.
(![]() )當點
)當點![]() 滿足
滿足![]() 時,求證:直線
時,求證:直線![]() 平面
平面![]() .
.
(![]() )當點
)當點![]() 是線段
是線段![]() 中點時,求直線
中點時,求直線![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A、B、C所對的邊分別為a、b、c,f (x)=sin(2x﹣A) (x∈R),函數f(x)的圖象關于點( ![]() ,0)對稱.
,0)對稱.
(1)當x∈(0, ![]() )時,求f (x)的值域;
)時,求f (x)的值域;
(2)若a=7且sinB+sinC= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司采用招考方式引進人才,規定必須在![]() ,三個測試點中任意選取兩個進行測試,若在這兩個測試點都測試合格,則可參加面試,否則不被錄用,已知考生在每測試個點測試結果互不影響,若考生小李和小王一起前來參加招考,小李在測試點
,三個測試點中任意選取兩個進行測試,若在這兩個測試點都測試合格,則可參加面試,否則不被錄用,已知考生在每測試個點測試結果互不影響,若考生小李和小王一起前來參加招考,小李在測試點![]() 測試合格的概率分別為
測試合格的概率分別為![]() ,小王在上述三個測試點測試合格的概率都是
,小王在上述三個測試點測試合格的概率都是![]() .
.
(1)問小李選擇哪兩個測試點測試才能使得可以參加面試的可能性最大?請說明理由;
(2)假設小李選擇測試點![]() 進行測試,小王選擇測試點
進行測試,小王選擇測試點![]() 進行測試,記
進行測試,記![]() 為兩人在各測試點測試合格的測試點個數之和,求隨機變量
為兩人在各測試點測試合格的測試點個數之和,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com