
【題目】以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程是ρ=2,矩形ABCD內接于曲線C1 , A,B兩點的極坐標分別為(2, ![]() )和(2,
)和(2, ![]() ),將曲線C1上所有點的橫坐標不變,縱坐標縮短為原來的一半,得到曲線C2 .
),將曲線C1上所有點的橫坐標不變,縱坐標縮短為原來的一半,得到曲線C2 .
(1)寫出C,D的直角坐標及曲線C2的參數方程;
(2)設M為C2上任意一點,求|MA|2+|MB|2+|MC|2+|MD|2的取值范圍.
【答案】
(1)解:曲線C1的極坐標方程是ρ=2,矩形ABCD內接于曲線C1,A,B兩點的極坐標分別為(2, ![]() )和(2,
)和(2, ![]() ),利用對稱性可得:C
),利用對稱性可得:C ![]() ,D
,D ![]() ,分別化為直角坐標:C
,分別化為直角坐標:C ![]() ,D
,D ![]() .
.
曲線C1的極坐標方程是ρ=2,化為直角坐標方程:x2+y2=4.
設曲線C2.上的任意一點坐標P(x,y),曲線C1的任意一點P′(x′,y′),則 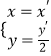 ,可得
,可得 ![]() .代入(x′)2+(y′)2=4,得x2+4y2=4,其參數方程為:
.代入(x′)2+(y′)2=4,得x2+4y2=4,其參數方程為: ![]()
(2)解:A ![]() ,B
,B ![]() .設M(2cosθ,sinθ).
.設M(2cosθ,sinθ).
|MA|2+|MB|2+|MC|2+|MD|2= ![]() +
+ ![]() +(sinθ﹣1)2+
+(sinθ﹣1)2+ ![]() +(sinθ+1)2+
+(sinθ+1)2+ ![]() +(sinθ+1)2
+(sinθ+1)2
=12cos2θ+20∈[20,32]
【解析】(1)利用對稱性可得:C ![]() ,D
,D ![]() ,分別化為直角坐標.曲線C1的極坐標方程是ρ=2,利用互化公式可得直角坐標方程.設曲線C2 . 上的任意一點坐標P(x,y),曲線C1的任意一點P′(x′,y′),則
,分別化為直角坐標.曲線C1的極坐標方程是ρ=2,利用互化公式可得直角坐標方程.設曲線C2 . 上的任意一點坐標P(x,y),曲線C1的任意一點P′(x′,y′),則 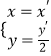 ,可得
,可得 ![]() .代入圓的方程可得x2+4y2=4,可得參數方程.(2)A
.代入圓的方程可得x2+4y2=4,可得參數方程.(2)A ![]() ,B
,B ![]() .設M(2cosθ,sinθ).利用兩點之間的距離公式、三角函數的基本關系式及其值域即可得出.
.設M(2cosθ,sinθ).利用兩點之間的距離公式、三角函數的基本關系式及其值域即可得出.


科目:高中數學 來源: 題型:
【題目】(1)求經過直線l1:x+3y-3=0,l2:x-y+1=0的交點且平行于直線2x+y-3=0的直線方程.
(2)求證:不論m取什么實數,直線(2m-1)x+(m+3)y-(m-11)=0都經過一個定點,并求出這個定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過右焦點作垂直于橢圓長軸的直線交橢圓于
,過右焦點作垂直于橢圓長軸的直線交橢圓于![]() 兩點,且
兩點,且![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2) 設直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,若
兩點,若![]() .
.
①求![]() 的值;
的值;
②求![]() 的面積
的面積![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() x2+(a+1)x+2ln(x﹣1).
x2+(a+1)x+2ln(x﹣1).
(1)若曲線y=f(x)在點(2,f(2))處的切線與直線2x﹣y+1=0平行,求出這條切線的方程;
(2)討論函數f(x)的單調區間;
(3)若對于任意的x∈(1,+∞),都有f(x)<﹣2,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盒子里裝有大小質量完全相同且分別標有數字1、2、3、4的四個小球,從盒子里隨機摸出兩個小球,那么事件“摸出的小球上標有的數字之和大于數字之積”的概率是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點到準線的距離為
的焦點到準線的距離為![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,過這兩點分別作拋物線
兩點,過這兩點分別作拋物線![]() 的切線,且這兩條切線相交于點
的切線,且這兩條切線相交于點![]() .
.
(1)若![]() 的坐標為
的坐標為![]() ,求
,求![]() 的值;
的值;
(2)設線段![]() 的中點為
的中點為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,過
,過![]() 的直線
的直線![]() 與線段
與線段![]() 為直徑的圓相切,切點為
為直徑的圓相切,切點為![]() ,且直線
,且直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx﹣ ![]() x2﹣x+a(a∈R).
x2﹣x+a(a∈R).
(1)當a=0時,求f(x)的單調區間;
(2)若函數f(x)在其定義域內有兩個不同的極值點.
(ⅰ)求a的取值范圍;
(ⅱ)設兩個極值點分別為x1 , x2 , 證明:x1x2>e2 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com