
 中,D、E分別是BC和
中,D、E分別是BC和 的中點,已知AB=AC=AA1=4,ÐBAC=90°.
的中點,已知AB=AC=AA1=4,ÐBAC=90°.
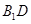 ⊥平面
⊥平面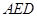 ;
;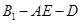 的余弦值;
的余弦值;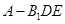 的體積.
的體積. (3)8
(3)8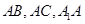 建立三維空間坐標系.下面重點分析法2
建立三維空間坐標系.下面重點分析法2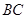 的長,而要證明
的長,而要證明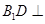 面
面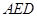 ,只需要證明
,只需要證明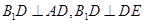 ,首先可以三次利用勾股定理把
,首先可以三次利用勾股定理把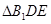 的三條邊長求出,再利用勾股定理證明
的三條邊長求出,再利用勾股定理證明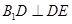 ,線段
,線段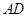 為等腰直角三角形ABC的三線合一即有
為等腰直角三角形ABC的三線合一即有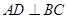 ,可得到
,可得到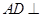 面
面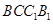 ,進而得到
,進而得到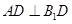 ,即可通過線線垂直證明
,即可通過線線垂直證明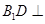 面DAE.
面DAE.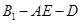 的余弦值,需要作出該二面角的平面角,為此過D做DM⊥AE于點M,連接B1M.,根據第一問有
的余弦值,需要作出該二面角的平面角,為此過D做DM⊥AE于點M,連接B1M.,根據第一問有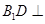 面AED且
面AED且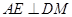 可以得到
可以得到 面
面 ,則
,則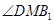 即為所求二面角的平面角,即該角的余弦值為
即為所求二面角的平面角,即該角的余弦值為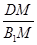 .利用勾股定理即可得到
.利用勾股定理即可得到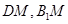 的長,進而得到二面角的余弦值.
的長,進而得到二面角的余弦值.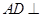 面
面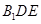 ,則該三棱錐可以以
,則該三棱錐可以以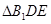 作為底面,高為
作為底面,高為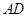 來求的體積,而AD和三角形的面積都可以用勾股定理求的.
來求的體積,而AD和三角形的面積都可以用勾股定理求的.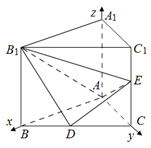
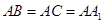 =4,所以A(0,0,0),B(4,0,0),E(0,4,2),D(2,2,0),B1(4,0,4). (1分)
=4,所以A(0,0,0),B(4,0,0),E(0,4,2),D(2,2,0),B1(4,0,4). (1分) ,
,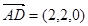 ,
,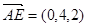 . (2分)
. (2分)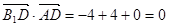 ,所以
,所以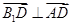 ,即
,即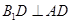 . (3分)
. (3分) ,所以
,所以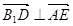 ,即
,即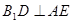 . (4分)
. (4分)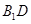 ⊥平面
⊥平面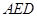 . (5分)
. (5分) 為平面AED的一個法向量. (6分)
為平面AED的一個法向量. (6分)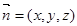 ,因為
,因為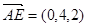 ,
,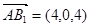 ,
, ,得
,得 ,令y=1,得x=2,z=-2.即
,令y=1,得x=2,z=-2.即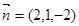 .(7分)
.(7分)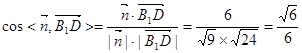 , (8分)
, (8分)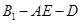 的余弦值為
的余弦值為 . (9分)
. (9分)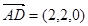 ,
,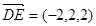 ,得
,得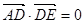 ,所以AD⊥DE. (10分)
,所以AD⊥DE. (10分)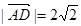 ,
,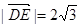 ,得
,得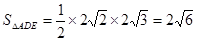 . (11分)
. (11分)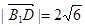 , (12分)
, (12分)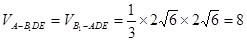 . (13分)
. (13分) 平面ABC,
平面ABC,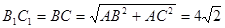 ,
,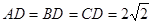 ,
,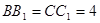 ,
,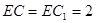 .
.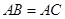 ,D為BC的中點,∴AD⊥BC.
,D為BC的中點,∴AD⊥BC. 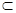 平面ABC,∴AD⊥B1B.
平面ABC,∴AD⊥B1B. 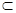 平面B1BCC1,且BC∩B1B=B,所以AD⊥平面B1BCC1.
平面B1BCC1,且BC∩B1B=B,所以AD⊥平面B1BCC1.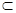 平面B1BCC1,故B1D⊥AD . (2分)
平面B1BCC1,故B1D⊥AD . (2分) ,
,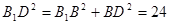 ,
,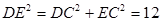 ,
,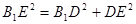 ,所以
,所以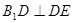 . (4分)
. (4分)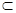 平面AED,且AD∩DE=E,故
平面AED,且AD∩DE=E,故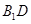 ⊥平面
⊥平面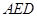 . (5分)
. (5分)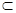 平面AED,得AE ⊥B1D.
平面AED,得AE ⊥B1D.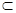 平面B1DM,且B1D∩DM=D,故AE⊥平面B1DM.
平面B1DM,且B1D∩DM=D,故AE⊥平面B1DM. 平面B1DM,所以B1M⊥AE.
平面B1DM,所以B1M⊥AE. 平面B1BCC1,所以AD⊥DE.
平面B1BCC1,所以AD⊥DE.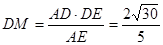 , (8分)
, (8分)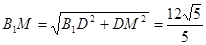 ,
,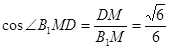 ,即二面角B1—AE—D的余弦值為
,即二面角B1—AE—D的余弦值為 . (9分)
. (9分)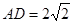 . (10分)
. (10分)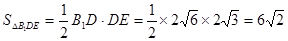 . (11分)
. (11分)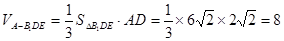 . (13分)
. (13分)

科目:高中數學 來源:不詳 題型:解答題

 中,
中, 底面
底面 ,
, ,E、F分別是棱
,E、F分別是棱 的中點.
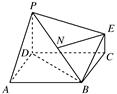
的中點.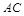 上的點
上的點 滿足平面
滿足平面 //平面
//平面 ,試確定點
,試確定點 的位置,并說明理由;
的位置,并說明理由; ⊥A1C.
⊥A1C.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的底面是邊長為2的正三角形,且側棱垂直于底面,側棱長是,D是AC的中點。
的底面是邊長為2的正三角形,且側棱垂直于底面,側棱長是,D是AC的中點。
 平面
平面 ;
; 的大小;
的大小; 與平面
與平面 所成的角的正弦值.
所成的角的正弦值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

 平面
平面 .
. 平面
平面
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
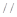 平面
平面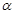 ,E,F分別是線段AD和BC的中點,當正四面體繞以AB為軸旋轉時,線段EF在平面
,E,F分別是線段AD和BC的中點,當正四面體繞以AB為軸旋轉時,線段EF在平面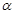 上的射影
上的射影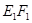 長的范圍是( )
長的范圍是( )A.[0, ] ] | B.[ , , ] ] |
C.[ , , ] ] | D.[ , , ] ] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com