【題目】如圖，在四棱錐
中， 
底面
，底面
為正方形， 
， 
分別是
的中點.
（Ⅰ）求證： 
；
（Ⅱ）求
與平面
所成角的正弦值.
【答案】（Ⅰ）見解析；（Ⅱ） 
.
【解析】試題分析：
(Ⅰ)由題意可證得
， 
，則
平面
，由線面垂直的性質有
，由三角形中位線的性質可得
，則
(Ⅱ)（方法一）
為
軸，以
為
軸，以
為
軸，建立空間直角坐標系，計算可得
平面
的一個法向量
，則
直線
與平面
所成角的正弦值為
.
（方法二）由等體積法可得點
到平面
的距離
，據此可得
與平面
所成角的正弦值為
.
試題解析：
（Ⅰ）因為
底面
， 
平面
，所以
又因為正方形
中， 
， 
所以
平面
又因為
平面
，所以
因為
分別是
、
的中點，所以
所以
（Ⅱ）（方法一）由（Ⅰ）可知， 
， 
， 
兩兩垂直，以
為
軸，以
為
軸，以
為
軸，設
，
， 
， 
， 
， 
， 
， 
設平面
的一個法向量
，
，解得
設直線
與平面
所成角為
，則
（方法二）設點
到平面
的距離為
等體積法求出
設直線
與平面
所成角為
， 
小學教材完全解讀系列答案科目：高中數學 來源： 題型：
【題目】某大學為調查來自南方和北方的同齡大學生的身高差異，從2016級的年齡在18～19歲之間的大學生中隨機抽取了來自南方和北方的大學生各10名，測量他們的身高，量出的身高如下(單位：cm)：
南方：158，170，166，169，180，175，171，176，162，163.
北方：183，173，169，163，179，171，157，175，184，166.
(1)根據抽測結果，畫出莖葉圖，對來自南方和北方的大學生的身高作比較，寫出統計結論．
(2)設抽測的10名南方大學生的平均身高為
cm，將10名南方大學生的身高依次輸入如圖所示的程序框圖進行運算，問輸出的s大小為多少？并說明s的統計學意義。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設有下面四個命題
p1：若復數z滿足 
∈R，則z∈R；
p2：若復數z滿足z2∈R，則z∈R；
p3：若復數z1 ， z2滿足z1z2∈R，則z1= 
；
p4：若復數z∈R，則 
∈R．
其中的真命題為（ ）
A.p1 ， p3
B.p1 ， p4
C.p2 ， p3
D.p2 ， p4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】交通指數是交通擁堵指數的簡稱，是綜合反映道路網暢通或擁堵的概念，記交通指數為T．其
范圍為[0，10]，分別有五個級別：T∈[0，2）暢通;T∈[2，4)基本暢通; T∈[4，6）輕度擁堵; T∈[6，8)中度擁堵；T∈[8，10]嚴重擁堵，晚高峰時段(T≥2)，從某市交通指揮中心選取了市區20個交通路段，依據其交通指數數據繪制的部分直方圖如圖所示．
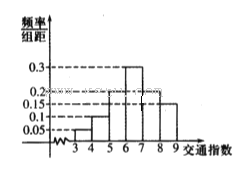
(1)請補全直方圖，并求出輕度擁堵、中度擁堵、嚴重擁堵路段各有多少個？
(2)用分層抽樣的方法從交通指數在[4，6），[6，8），[8，l0]的路段中共抽取6個路段，求依次抽取的三個級別路段的個數；
(3)從(2)中抽出的6個路段中任取2個，求至少一個路段為輕度擁堵的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
+ 
=1（a＞b＞0），四點P1（1，1），P2（0，1），P3（﹣1， 
），P4（1， ）中恰有三點在橢圓C上．（12分）
（1）求C的方程；
（2）設直線l不經過P2點且與C相交于A，B兩點．若直線P2A與直線P2B的斜率的和為﹣1，證明：l過定點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn.已知2Sn＝3n＋3.
(1)求{an}的通項公式；
(2)若數列{bn}滿足anbn＝log3an，求{bn}的前n項和Tn.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】△ABC的內角A，B，C的對邊分別為a，b，c，已知sinB+sinA（sinC﹣cosC）=0，a=2，c= 
，則C=（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
