
【題目】已知函數![]() .
.
(1)當![]() 時,證明:
時,證明: ![]() 為偶函數;
為偶函數;
(2)若![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() ,求實數
,求實數![]() 的取值范圍,使
的取值范圍,使![]() 在
在![]() 上恒成立.
上恒成立.
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)代入![]() ,根據函數奇偶性的定義,即可判定
,根據函數奇偶性的定義,即可判定![]() 為偶函數;
為偶函數;
(2)利用函數單調性的定義,求得函數![]() 在
在![]() 上單調遞增,進而得到
上單調遞增,進而得到![]() 對任意的
對任意的![]() 恒成立,即可求解實數
恒成立,即可求解實數![]() 的取值范圍;
的取值范圍;
(3)由(1)、(2)知函數![]() 的最小值
的最小值![]() ,進而得
,進而得![]() ,設
,設![]() ,得不等式
,得不等式![]() 恒成立,等價于
恒成立,等價于![]() ,進而
,進而![]() 恒成立,利用二次函數的性質即可求解實數
恒成立,利用二次函數的性質即可求解實數![]() 的取值范圍.
的取值范圍.
試題解析:
(1)當![]() 時,
時, ![]() ,定義域
,定義域![]() 關于原點對稱,
關于原點對稱,
而![]() ,說明
,說明![]() 為偶函數;
為偶函數;
(2)在![]() 上任取
上任取![]() 、
、![]() ,且
,且![]() ,
,
則![]() ,
,
因為![]() ,函數
,函數![]() 為增函數,得
為增函數,得![]() ,
, ![]() ,
,
而![]() 在
在![]() 上單調遞增,得
上單調遞增,得![]() ,
, ![]() ,
,
于是必須![]() 恒成立,
恒成立,
即![]() 對任意的
對任意的![]() 恒成立,
恒成立,
![]() ;
;
(3)由(1)、(2)知函數![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,
上遞增,
其最小值![]() ,
,
且![]() ,
,
設![]() ,則
,則![]() ,
, ![]()
于是不等式![]() 恒成立,等價于
恒成立,等價于![]() ,
,
即![]() 恒成立,
恒成立,
而![]() ,僅當
,僅當![]() ,即
,即![]() 時取最大值
時取最大值![]() ,
,
故![]()


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)=ex﹣ax2﹣2x+b(e為自然對數的底數,a,b∈R).
(Ⅰ)設f′(x)為f(x)的導函數,證明:當a>0時,f′(x)的最小值小于0;
(Ⅱ)若a<0,f(x)>0恒成立,求符合條件的最小整數b.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,EP交圓于E,C兩點,PD切圓于D,G為CE上一點且PG=PD,連接DG并延長交圓于點A,作弦AB垂直EP,垂足為F. 
(1)求證:BD⊥AD;
(2)若AC=BD,AB=6,求弦DE的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某小區抽取100戶居民進行月用電量調查,發現其用電量都在50度至350度之間,頻率分布直方圖如圖所示. 
(1)根據直方圖求x的值,并估計該小區100戶居民的月均用電量(同一組中的數據用該組區間的中點值作代表);
(2)從該小區已抽取的100戶居民中,隨機抽取月用電量超過250度的3戶,參加節約用電知識普及講座,其中恰有ξ戶月用電量超過300度,求ξ的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx﹣ax2+(2a﹣1)x.
(1)若a= ![]() ,求函數f(x)的單調區間;
,求函數f(x)的單調區間;
(2)若x∈[1,+∞)時恒有f(x)≤a﹣1,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”是騰訊開發的一個記錄跑步或行走情況(步數里程)的公眾號用戶通過該公眾號可查看自己某時間段的運動情況.某人根據2018年1月至2018年11月期間每月離步的里程(單位:十公里)的數據繪制了下面的折線圖.根據該折線圖,下列結論正確的是( )

A.月跑步里程逐月增加
B.月跑步里程最大值出現在10月
C.月跑步里程的中位數為5月份對應的里程數
D.1月至5月的月跑步里程相對于6月至11月波動性更小,變化比較平穩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣lnx+a﹣1,g(x)= ![]() +ax﹣xlnx,其中a>0.
+ax﹣xlnx,其中a>0.
(1)求f(x)的單調區間;
(2)當x≥1時,g(x)的最小值大于 ![]() ﹣lna,求a的取值范圍.
﹣lna,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據某市供電公司數據,2019年1月份市新能源汽車充電量約270萬度,同比2018年增長![]() ,為了增強新能源汽車的推廣運用,政府加大了充電樁等基礎設施的投入.現為了了解該城市充電樁等基礎設施的使用情況,隨機選取了200個駕駛新能源汽車的司機進行問卷調查,根據其滿意度評分值(百分制)按照
,為了增強新能源汽車的推廣運用,政府加大了充電樁等基礎設施的投入.現為了了解該城市充電樁等基礎設施的使用情況,隨機選取了200個駕駛新能源汽車的司機進行問卷調查,根據其滿意度評分值(百分制)按照![]() ,
,![]() ,…,
,…,![]() 分成5組,制成如圖所示的頻率分布直方圖.
分成5組,制成如圖所示的頻率分布直方圖.
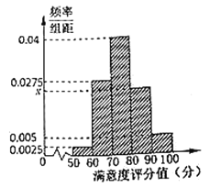
(1)求圖中![]() 的值并估計樣本數據的中位數;
的值并估計樣本數據的中位數;
(2)已知滿意度評分值在![]() 內的男女司機人數比為
內的男女司機人數比為![]() ,從中隨機抽取2人進行座談,求2人均為女司機的概率.
,從中隨機抽取2人進行座談,求2人均為女司機的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4﹣4:極坐標與參數方程
極坐標系與直角坐標系xOy有相同的長度單位,以原點O為極點,以x軸正半軸為極軸.已知曲線C1的極坐標方程為 ![]() ,曲線C2的極坐標方程為ρsinθ=a(a>0),射線
,曲線C2的極坐標方程為ρsinθ=a(a>0),射線 ![]() ,
, ![]() 與曲線C1分別交異于極點O的四點A,B,C,D.
與曲線C1分別交異于極點O的四點A,B,C,D.
(Ⅰ)若曲線C1關于曲線C2對稱,求a的值,并把曲線C1和C2化成直角坐標方程;
(Ⅱ)求|OA||OC|+|OB||OD|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com