分析:根據題意,建立空間坐標系得出各點的坐標,給出各點的坐標,
(1)求出兩個平面的法向量,利用公式求稅二面角的余弦;
(2)利用向量證明直線的方向向量與平面的法向量垂直,再結合線不在面內得出線面平行;
(3)點到面的距離可由轉化為此點與面內一點對應的向量在面的法向量上的投影長,故設出點M的坐標,用點M的坐標表示出此投影長,令其為
,解出點M的坐標,即可求出點M的位置
解答: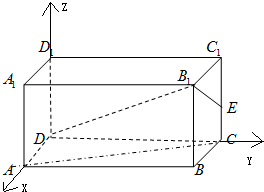
解:建如圖的立空間坐標系可得:D(0,0,0),A(1,0,0),C(0,2,0),B(1,2,0),A
1(1,0,1),D
1(0,0,1),C
1(0,2,1),B
1(1,2,1),由中點坐標公式可得E(0,2,
),
(1)設面DB
1E的法向量是
=(x,y,z),又
=(0,2,
),
=(1,2,1),由
得
,令y=1,得x=2,z=-4
故有
=(2,1,-4),同理可求得面BB
1E的法向量為
=(0,1,0),故兩平面所成的稅二面角的余弦cosθ=|
|=
(2)由題意,AC的方向向量的坐標是
=(-1,2,0),又面DB
1E的法向量
=(2,1,-4),由于
•=-2+2=0,故
⊥,又AC不在面DB
1E內,故AC與面DB
1E的位置關系是平行.
(3)M是棱AB上一點,
設M(1,x,0),則
=(-1,-X,0),
由(1)面DB
1E的法向量
=(2,1,-4),M到面DB
1E的距離即向量
在DB
1E的法向量
上的投影長度,
故有d=|
|=|
=|
|即得|2+x|=3解得x=1,或x=-1(由圖知,此結論舍),
故M是AB的中點時,符合題意.
點評:本題考查二面角的平面角及求法,解題的關鍵是建立空間坐標系,利用向量法求證線面垂直,線面平行,以及求面面夾角,利用空間向量求解立體幾何中的線面,面面位置關系及求線面角,二面角,是空間向量的重要應用,引入空間向量,大大降低了求解立體幾何問題時的問題時的推理難度,使得思考變得容易,但此法也有不足,從解題過程可以看出,用空間向量法解立體幾何問題,運算量不少,計算時要嚴謹,莫因運算出錯導致解題失敗.本題中將求點到面的距離的問題轉化為求向量在面的法向量上的投影長,方法新穎,注意理解掌握.

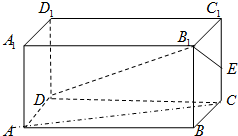 如圖,在長方體ABCD-A1B1C1D1中,AD=AA1=1,AB=2.E是CC1的中點,
如圖,在長方體ABCD-A1B1C1D1中,AD=AA1=1,AB=2.E是CC1的中點, 解:建如圖的立空間坐標系可得:D(0,0,0),A(1,0,0),C(0,2,0),B(1,2,0),A1(1,0,1),D1(0,0,1),C1(0,2,1),B1(1,2,1),由中點坐標公式可得E(0,2,
解:建如圖的立空間坐標系可得:D(0,0,0),A(1,0,0),C(0,2,0),B(1,2,0),A1(1,0,1),D1(0,0,1),C1(0,2,1),B1(1,2,1),由中點坐標公式可得E(0,2,

 名校課堂系列答案
名校課堂系列答案 如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側面積的最大值等于( )
如圖,定義八個頂點都在某圓柱的底面圓周上的長方體叫做圓柱的內接長方體,圓柱也叫長方體的外接圓柱.設長方體ABCD-A1B1C1D1的長、寬、高分別為a,b,c(其中a>b>c),那么該長方體的外接圓柱側面積的最大值等于( )
![]() B.
B.![]() C.
C.![]() D.1
D.1
![]() B.
B.![]() C.
C.![]() D.1
D.1 .
. 
 ,AA1 =
,AA1 = ,M為側棱CC1上一點,AM⊥BA1.
,M為側棱CC1上一點,AM⊥BA1.