
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點.
的中點.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】為考察高中生的性別與是否喜歡數學課程之間的關系,在我市某普通中學高中生中隨機抽取200名學生,得到如下2×2列聯表:
喜歡數學課 | 不喜歡數學課 | 合計 | |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合計 | 50 | 150 | 200 |
經計算K2≈6.06,根據獨立性檢驗的基本思想,約有(填百分數)的把握認為“性別與喜歡數學課之間有關系”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費x(單位:千元)對年銷售量y(單位:t)和年利潤z(單位:千元)的影響.對近8年的年宣傳費xi和年銷售量yi(i=1,2,…,8)數據作了初步處理,得到下面的散點圖及下面一些統計量的值.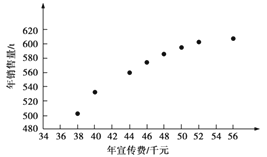
|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中 ![]() ,
, ![]() .
.
附:對于一組數據(u1,v1),(u2,v2),…,(un,vn),其回歸直線v=α+βu的斜率和截距的最下二乘估計分別為 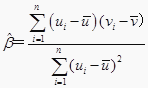 ,
, ![]() .
.
(1)根據散點圖判斷,y=a+bx與 ![]() 哪一個適宜作為年銷售量y關于年宣傳費x的回歸方程類型?(給出判斷即可,不必說明理由)
哪一個適宜作為年銷售量y關于年宣傳費x的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立y關于x的回歸方程;
(3)已知這種產品的年利潤z與x,y的關系為z=0.2y-x.根據(2)的結果回答下列問題:
①年宣傳費x=49時,年銷售量及年利潤的預報值時多少?
②年宣傳費x為何值時,年利潤的預報值最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海上某貨輪在A處看燈塔B在貨輪的北偏東75°,距離為12![]() 海里;在A處看燈塔C在貨輪的北偏西30°,距離為8
海里;在A處看燈塔C在貨輪的北偏西30°,距離為8![]() 海里;貨輪向正北由A處行駛到D處時看燈塔B在貨輪的北偏東120°.(要畫圖)
海里;貨輪向正北由A處行駛到D處時看燈塔B在貨輪的北偏東120°.(要畫圖)
(1)A處與D處之間的距離;
(2)燈塔C與D處之間的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著移動互聯網的快速發展,基于互聯網的共享單車應運而生.某市場研究人員為了了解共享單車運營公司![]() 的經營狀況,對該公司最近六個月內的市場占有率進行了統計,并繪制了相應的拆線圖.
的經營狀況,對該公司最近六個月內的市場占有率進行了統計,并繪制了相應的拆線圖.

(1)由拆線圖可以看出,可用線性回歸模型擬合月度市場占有率![]() 與月份代碼
與月份代碼![]() 之間的關系.求
之間的關系.求![]() 關于
關于![]() 的線性回歸方程,并預測
的線性回歸方程,并預測![]() 公司2017年4月份(即
公司2017年4月份(即![]() 時)的市場占有率;
時)的市場占有率;
(2)為進一步擴大市場,公司擬再采購一批單車.現有采購成本分別為1000元/輛和1200元/輛的![]() 兩款車型可供選擇,按規定每輛單車最多使用4年,但由于多種原因(如騎行頻率等)會導致車輛報廢年限各不相同.考慮到公司運營的經濟效益,該公司決定先對兩款車型的單車各100輛進行科學模擬測試,得到兩款單車使用壽命頻數表如下:
兩款車型可供選擇,按規定每輛單車最多使用4年,但由于多種原因(如騎行頻率等)會導致車輛報廢年限各不相同.考慮到公司運營的經濟效益,該公司決定先對兩款車型的單車各100輛進行科學模擬測試,得到兩款單車使用壽命頻數表如下:
車型 報廢年限 | 1年 | 2年 | 3年 | 4年 | 總計 |
| 20 | 35 | 35 | 10 | 100 |
| 10 | 30 | 40 | 20 | 100 |
經測算,平均每輛單車每年可以帶來收入500元.不考慮除采購成本之外的其他成本,假設每輛單車的使用壽命都是整年,且以頻率作為每輛單車使用壽命的概率.如果你是![]() 公司的負責人,以每輛單車產生利潤的期望值為決策依據,你會選擇采購哪款車型?
公司的負責人,以每輛單車產生利潤的期望值為決策依據,你會選擇采購哪款車型?
(參考公式:回歸直線方程為![]() ,其中
,其中 )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com