
【題目】下列命題中,真命題的個數是( )
①若“p∨q”為真命題,則“p∧q”為真命題;
②“a∈(0,+∞),函數y=![]() 在定義域內單調遞增”的否定;
在定義域內單調遞增”的否定;
③l為直線,α,β為兩個不同的平面,若l⊥β,α⊥β,則l∥α;
④“x∈R,![]() ≥0”的否定為“
≥0”的否定為“![]() R,
R,![]() <0”.
<0”.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
利用復合命題的真假判斷①的正誤;利用指數函數的單調性判斷②的正誤;直線與平面垂直關系判斷③的正誤;根據全稱命題的否定的寫法判斷④的正誤;
①若“p∨q”為真命題,可知兩個命題至少一個是真命題,判斷為“p∧q”有可能是假命題,不正確;
②“a∈(0,+∞),函數y=ax在定義域內單調遞增”的否定:“a∈(0,+∞),函數y=ax在定義域內不是單調遞增的”;例如a=![]() ,
,![]() 在定義域內單調遞減;所以②正確;
在定義域內單調遞減;所以②正確;
③l為直線,α,β為兩個不同的平面,若l⊥β,α⊥β,則l∥α;也可能lα,所以③不正確;
④“x∈R,x2≥0”的否定的正確寫法為“![]() ,使得
,使得![]() <0”.故選項不滿足命題的否定形式,所以④不正確;
<0”.故選項不滿足命題的否定形式,所以④不正確;
只有②是真命題;
故選:A.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:
【題目】某幼兒園雛鷹班的生活老師統計2018年上半年每個月的20日的晝夜溫差![]() ,
,![]() 和患感冒的小朋友人數(
和患感冒的小朋友人數(![]() /人)的數據如下:
/人)的數據如下:
溫差 |
|
|
|
|
|
|
患感冒人數 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)請用相關系數加以說明是否可用線性回歸模型擬合![]() 與
與![]() 的關系;
的關系;
(Ⅱ)建立![]() 關于
關于![]() 的回歸方程(精確到
的回歸方程(精確到![]() ),預測當晝夜溫差升高
),預測當晝夜溫差升高![]() 時患感冒的小朋友的人數會有什么變化?(人數精確到整數)
時患感冒的小朋友的人數會有什么變化?(人數精確到整數)
參考數據:![]() .參考公式:相關系數:
.參考公式:相關系數: ,回歸直線方程是
,回歸直線方程是![]() ,
, ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環.據此,某網站推出了關于生態文明建設進展情況的調查,大量的統計數據表明,參與調查者中關注此問題的約占80%.現從參與調查的人群中隨機選出![]() 人,并將這
人,并將這![]() 人按年齡分組:第1組
人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4 組
,第4 組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示
,得到的頻率分布直方圖如圖所示
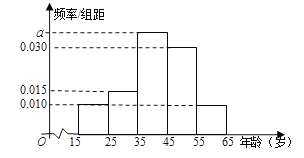
(1) 求![]() 的值
的值
(2)現在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行問卷調查,求在第1組已被抽到
人進行問卷調查,求在第1組已被抽到![]() 人的前提下,第3組被抽到
人的前提下,第3組被抽到![]() 人的概率;
人的概率;
(3)若從所有參與調查的人中任意選出![]() 人,記關注“生態文明”的人數為
人,記關注“生態文明”的人數為![]() ,求
,求![]() 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,動圓
,動圓![]() 與圓
與圓![]() 內切且與圓
內切且與圓![]() 外切.
外切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)已知![]() 與
與![]() 為平面內的兩個定點,過
為平面內的兩個定點,過![]() 點的直線
點的直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() =1(a>0,b>0)的右焦點為F,P,Q為雙曲線上關于原點對稱的兩點,若
=1(a>0,b>0)的右焦點為F,P,Q為雙曲線上關于原點對稱的兩點,若![]() =0,且∠POF<
=0,且∠POF<![]() ,則該雙曲線的離心率的取值范圍為______.
,則該雙曲線的離心率的取值范圍為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 為偶函數,且函數
為偶函數,且函數![]() 的圖象的兩相鄰對稱軸間的距離為
的圖象的兩相鄰對稱軸間的距離為![]() .
.
(1)求![]() 的值;
的值;
(2)將函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后,再將得到的圖象上各點的橫坐標伸長為原來的4倍,縱坐標不變,得到函數
個單位長度后,再將得到的圖象上各點的橫坐標伸長為原來的4倍,縱坐標不變,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 的單調遞減區間.
的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①集合{x∈N|x3=x}用列舉法表示為{-1,0,1};
②實數集可以表示為{x|x為所有實數}或{R};
③方程組![]() 的解集為{x=1,y=2}.
的解集為{x=1,y=2}.
其中正確的有( )
A.3個B.2個
C.1個D.0個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com