
【題目】設f'(x)是函數f(x)的導數,f'(x)是函數f'(x)的導數,若方程f'(x)=0有實數解x0 , 則稱點(x0 , f(x0))為函數f(x)的拐點.某同學經過探究發現:任何一個三次函數f(x)=ax3+bx2+cx+d(a≠0)都有拐點,任何一個三次函數都有對稱中心,且拐點就是對稱中心,
設函數g(x)=x3﹣3x2+4x+2,利用上述探究結果
計算: ![]() =
=
 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(cos
=(cos ![]() ﹣1),
﹣1), ![]() =(
=( ![]() sin
sin ![]() ,cos2
,cos2 ![]() ),函數f(x)=
),函數f(x)= ![]() +1.
+1.
(1)若x∈[ ![]() ,π],求f(x)的最小值及對應的x的值;
,π],求f(x)的最小值及對應的x的值;
(2)若x∈[0, ![]() ],f(x)=
],f(x)= ![]() ,求sinx的值.
,求sinx的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]() 與
與 ![]() (其中
(其中 ![]() )在
)在 ![]() 上的單調性正好相反,回答下列問題:
上的單調性正好相反,回答下列問題:
(1)對于 ![]() ,
, ![]() ,不等式
,不等式 ![]() 恒成立,求實數
恒成立,求實數 ![]() 的取值范圍;
的取值范圍;
(2)令 ![]() ,兩正實數
,兩正實數 ![]() 、
、 ![]() 滿足
滿足 ![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}的前n項a1 , a2 , …,an(n∈N*)組成集合An={a1 , a2 , …,an},從集合An中任取k(k=1,2,3,…,n)個數,其所有可能的k個數的乘積的和為Tk(若只取一個數,規定乘積為此數本身),例如:對于數列{2n﹣1},當n=1時,A1={1},T1=1;n=2時,A2={1,3},T1=1+3,T2=13;
(1)若集合An={1,3,5,…,2n﹣1},求當n=3時,T1 , T2 , T3的值;
(2)若集合An={1,3,7,…,2n﹣1},證明:n=k時集合Ak的Tm與n=k+1時集合Ak+1的Tm(為了以示區別,用Tm′表示)有關系式Tm′=(2k+1﹣1)Tm﹣1+Tm , 其中m,k∈N*,2≤m≤k;
(3)對于(2)中集合An . 定義Sn=T1+T2+…+Tn , 求Sn(用n表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=f'(1)ex﹣1﹣f(0)x+ ![]() 的導數,e為自然對數的底數)g(x)=
的導數,e為自然對數的底數)g(x)= ![]() +ax+b(a∈R,b∈R)
+ax+b(a∈R,b∈R)
(Ⅰ)求f(x)的解析式及極值;
(Ⅱ)若f(x)≥g(x),求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=|2x﹣1|+|5x﹣1|
(1)求f(x)>x+1的解集;
(2)若m=2﹣n,對m,n∈(0,+∞),恒有 ![]() 成立,求實數x的范圍.
成立,求實數x的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正三棱柱ABC﹣A1B1C1中,AB=1,BB1=2,求: 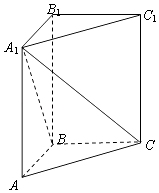
(1)異面直線B1C1與A1C所成角的大小;
(2)四棱錐A1﹣B1BCC1的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com