
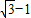 ,BC=
,BC=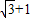 ,
,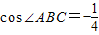 ,且△ACD的面積等于△ABC面積的3倍,求:
,且△ACD的面積等于△ABC面積的3倍,求: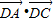 的值;
的值;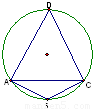
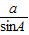 =
=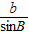 =
=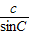 =2R,根據本題的已知條件,可知用正弦定理相對可行,故可由余弦定理求出AC,再由正弦定理求R.
=2R,根據本題的已知條件,可知用正弦定理相對可行,故可由余弦定理求出AC,再由正弦定理求R.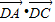 ,根據向量數量積的計算公式,我們要求出兩個向量模的積及夾角的余弦值,由∠B與∠D互補,夾角的余弦值易得,然后根據△ACD的面積等于△ABC面積的3倍,也可以得到兩個向量模的積,代入可得答案.
,根據向量數量積的計算公式,我們要求出兩個向量模的積及夾角的余弦值,由∠B與∠D互補,夾角的余弦值易得,然后根據△ACD的面積等于△ABC面積的3倍,也可以得到兩個向量模的積,代入可得答案.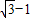 ,BC=
,BC=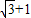 ,我們要求四邊形的周長,關鍵是要求出AD、CD邊的長,結合(2)結論和余弦定理,易得答案.
,我們要求四邊形的周長,關鍵是要求出AD、CD邊的長,結合(2)結論和余弦定理,易得答案.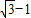 ,BC=
,BC=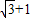 ,
,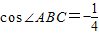 ,
,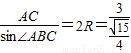 ,
,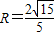 ;
; ,
,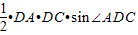 =
=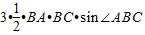
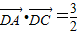 ;
;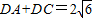 ,
,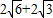 .
.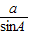 =
=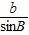 =
=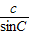 =2R;③如果圓為△ABC的內切圓,則根據面積公式S=
=2R;③如果圓為△ABC的內切圓,則根據面積公式S= •l•r(其中l表示三角形的周長).熟練掌握定理及公式是解本題的關鍵.
•l•r(其中l表示三角形的周長).熟練掌握定理及公式是解本題的關鍵. 

 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案科目:高中數學 來源: 題型:
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
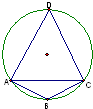 在半徑為R的圓的內接四邊形ABCD中,AB=
在半徑為R的圓的內接四邊形ABCD中,AB=| 3 |
| 3 |
| 1 |
| 4 |
| DA |
| DC |
查看答案和解析>>
科目:高中數學 來源:2010年江蘇省鹽城中學高考數學三模試卷(解析版) 題型:填空題
 .通過類比,我們可得結論:在空間,半徑為R的球的內接長方體中,以 的表面積為最大,最大值為 .
.通過類比,我們可得結論:在空間,半徑為R的球的內接長方體中,以 的表面積為最大,最大值為 .查看答案和解析>>
科目:高中數學 來源:2010年江蘇省連云港市東海高級中學高考數學考前猜題試卷(4)(解析版) 題型:解答題
 .通過類比,我們可得結論:在空間,半徑為R的球的內接長方體中,以 的表面積為最大,最大值為 .
.通過類比,我們可得結論:在空間,半徑為R的球的內接長方體中,以 的表面積為最大,最大值為 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com