
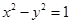 的焦點與橢圓
的焦點與橢圓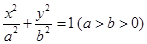 的焦點重合,且該橢圓的長軸長為
的焦點重合,且該橢圓的長軸長為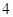 ,
, 是橢圓上的的動點.
是橢圓上的的動點.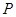 滿足:
滿足: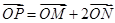 ,直線
,直線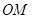 與
與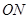 的斜率之積為
的斜率之積為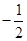 ,求證:存在定點
,求證:存在定點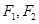 ,
,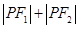 為定值,并求出
為定值,并求出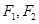 的坐標;
的坐標;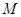 在第一象限,且點
在第一象限,且點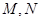 關于原點對稱,點
關于原點對稱,點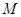 在
在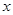 軸的射影為
軸的射影為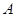 ,連接
,連接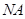 并延長交橢圓于
并延長交橢圓于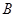 ,求證:以
,求證:以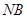 為直徑的圓經(jīng)過點
為直徑的圓經(jīng)過點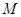 .
.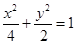 ;(2)存在
;(2)存在 ;(3)證明過程詳見試題解析.
;(3)證明過程詳見試題解析.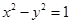 的焦點與橢圓
的焦點與橢圓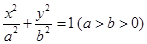 的焦點重合求出橢圓中的
的焦點重合求出橢圓中的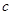 ,再由
,再由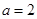 ,求出所求橢圓方程為
,求出所求橢圓方程為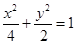 ;(2)先設
;(2)先設 ,由
,由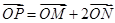 ,結合橢圓的標準方程可以得到
,結合橢圓的標準方程可以得到 使得
使得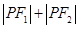 為定值;(3)要證明以
為定值;(3)要證明以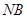 為直徑的圓經(jīng)過點
為直徑的圓經(jīng)過點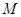 ,就是證明
,就是證明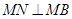 ,詳見解析.
,詳見解析. 的焦點為
的焦點為 ,
, 
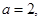

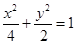
 ,由
,由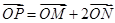 可得:
可得: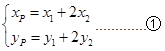
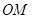 與
與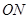 的斜率之積為
的斜率之積為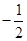 可得:
可得: ,即
,即
 …6分
…6分
 ,即
,即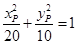
 ,使得動點P到兩定點距離和為定值
,使得動點P到兩定點距離和為定值 ;
;
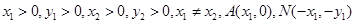
 斜率存在且滿足
斜率存在且滿足 .……③
.……③
 …⑤
…⑤  在橢圓
在橢圓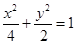 ,故
,故

 為直徑的圓經(jīng)過點
為直徑的圓經(jīng)過點 .
.

 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
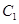 、拋物線
、拋物線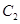 的焦點均在
的焦點均在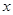 軸上,
軸上,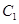 的中心和
的中心和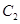 的頂點均為原點
的頂點均為原點 ,從每條曲線上取兩個點,將其坐標記錄如下:
,從每條曲線上取兩個點,將其坐標記錄如下: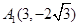 、
、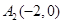 、
、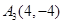 、
、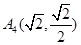 .
.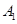 ,
,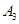 在拋物線
在拋物線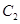 上,試求出
上,試求出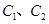 的標準方程;
的標準方程;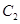 的焦點
的焦點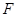 的坐標并求出橢圓
的坐標并求出橢圓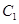 的離心率;
的離心率;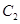 的焦點
的焦點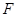 直線與橢圓
直線與橢圓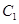 交不同兩點
交不同兩點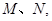 且滿足
且滿足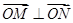 ,試求出直線的方程.
,試求出直線的方程.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
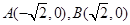 連線的斜率的積為定值
連線的斜率的積為定值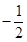 .
.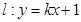 與曲線C交于M、N兩點,當|MN|=
與曲線C交于M、N兩點,當|MN|=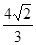 時,求直線l的方程.
時,求直線l的方程.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
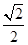 .
.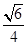 的任意兩點,E為線段AB的中點,射線OE交橢圓C于點P.設
的任意兩點,E為線段AB的中點,射線OE交橢圓C于點P.設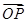 =t
=t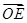 ,求實數(shù)t的值.
,求實數(shù)t的值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
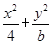 =1,直線l:y=mx+1,若對任意的m∈R,直線l與橢圓C恒有公共點,則實數(shù)b的取值范圍是( )
=1,直線l:y=mx+1,若對任意的m∈R,直線l與橢圓C恒有公共點,則實數(shù)b的取值范圍是( )| A.[1,4) | B.[1,+∞) | C.[1,4)∪(4,+∞) | D.(4,+∞) |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
 +
+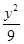 =1及以下3個函數(shù):①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函數(shù)圖像能等分該橢圓面積的函數(shù)個數(shù)有( )
=1及以下3個函數(shù):①f(x)=x;②f(x)=sin x;③f(x)=cos x.其中函數(shù)圖像能等分該橢圓面積的函數(shù)個數(shù)有( )| A.1個 | B.2個 |
| C.3個 | D.0個 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
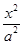 +
+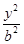 =1(a>b>0)的右焦點為F(3,0),過點F的直線交橢圓于A、B兩點.若AB的中點坐標為(1,-1),則E的方程為( ).
=1(a>b>0)的右焦點為F(3,0),過點F的直線交橢圓于A、B兩點.若AB的中點坐標為(1,-1),則E的方程為( ).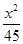 +
+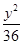 =1 B.
=1 B.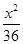 +
+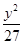 =1
=1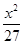 +
+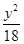 =1 D.
=1 D.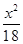 +
+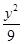 =1
=1查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
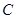 :
: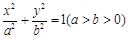 的短軸長為2,離心率為
的短軸長為2,離心率為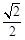 ,設過右焦點的直線
,設過右焦點的直線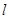 與橢圓
與橢圓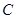 交于不同的兩點A,B,過A,B作直線
交于不同的兩點A,B,過A,B作直線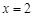 的垂線AP,BQ,垂足分別為P,Q.記
的垂線AP,BQ,垂足分別為P,Q.記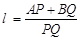 , 若直線l的斜率
, 若直線l的斜率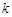 ≥
≥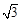 ,則
,則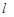 的取值范圍為 .
的取值范圍為 .查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com