
(1)求![]() 的極值;
的極值;
(2)當(dāng)a在什么范圍內(nèi)取值時,曲線![]() 與x軸僅有一個交點.
與x軸僅有一個交點.
解:(1)![]() =3x2-2x-1.
=3x2-2x-1.
若![]() =0,則x=-
=0,則x=-![]() ,1.
,1.
當(dāng)x變化時, ![]() ,
, ![]() 的變化情況如下表.
的變化情況如下表.
x | (-∞,- | - | (- | 1 | (1, +∞) |
| + | 0 | - | 0 | + |
所以![]() 的極大值是f(-
的極大值是f(-![]() )=
)=![]() +a,極小值是f(1)=a-1.
+a,極小值是f(1)=a-1.
(2)函數(shù)![]() =x3-x2-x+a=(x-1)2(x+1)+a-1.
=x3-x2-x+a=(x-1)2(x+1)+a-1.
由此可知x取足夠大的正數(shù)時,有![]() >0,x取足夠小的負(fù)數(shù)時有
>0,x取足夠小的負(fù)數(shù)時有![]() <0.
<0.
所以曲線![]() 與x軸至少有一個交點.
與x軸至少有一個交點.
結(jié)合![]() 的單調(diào)性可知.
的單調(diào)性可知.
當(dāng)![]() 的極大值
的極大值![]() +a<0,即a∈(-∞,-
+a<0,即a∈(-∞,-![]() )時,它的極小值也小于0,因此曲線
)時,它的極小值也小于0,因此曲線![]() 與x軸僅有一個交點,它在(1,+∞)上;
與x軸僅有一個交點,它在(1,+∞)上;
當(dāng)![]() 的極小值a-1>0,即a∈(1,+∞)時,它的極大值也大于0,因此曲線
的極小值a-1>0,即a∈(1,+∞)時,它的極大值也大于0,因此曲線![]() 與x軸僅有一個交點,它在(-∞,-
與x軸僅有一個交點,它在(-∞,-![]() )上.?
)上.?
所以當(dāng)a∈(-∞,-![]() )∪(1,+∞)時,曲線
)∪(1,+∞)時,曲線![]() 與x軸僅有一個交點.
與x軸僅有一個交點.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年四川省高三高考極限壓軸文科數(shù)學(xué)試卷(解析版) 題型:解答題
設(shè)a為實數(shù),函數(shù)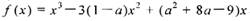 ,x
,x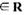
 (1) 當(dāng)a= 0時,求
(1) 當(dāng)a= 0時,求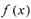 的極大值、極小值;
的極大值、極小值;
(2) 若x>0時,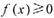 ,求a的取值范圍;.
,求a的取值范圍;.
(3) 若函數(shù)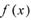 在區(qū)間(0,1)上是減函數(shù),求a的取值范圍.
在區(qū)間(0,1)上是減函數(shù),求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(本題滿分14分)設(shè)a為實數(shù),函數(shù)![]() ,x
,x![]()
(1) 當(dāng)a= 0時,求![]() 的極大值、極小值;
的極大值、極小值;
(2) 若x>0時,![]() ,求a的取值范圍;.
,求a的取值范圍;.
(3) 若函數(shù)![]() 在區(qū)間(0,1)上是減函數(shù),求a的取值范圍.
在區(qū)間(0,1)上是減函數(shù),求a的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com