【題目】函數f（x）是定義在R上的奇函數，對任意的x∈R，滿足f（x+1）+f（x）=0，且當0＜x＜1時，f（x）=2x ， 則f（﹣ 
）+f（4）= ．
【答案】﹣ 
【解析】解：∵f（x）是定義在R上的奇函數，對任意的x∈R，滿足f（x+1）+f（x）=0，
∴f（x+1）=﹣f（x），
則f（x+2）=﹣f（x+1）=f（x），
則函數f（x）是周期為2的周期函數，
則f（4）=f（0）=0，
∵當0＜x＜1時，f（x）=2x ，
∴f（﹣ 
）=f（﹣ +2）=f（﹣ 
）=﹣f（ ）=﹣ 
=﹣ ，
則f（﹣ ）+f（4）=﹣ +0=﹣ ，
所以答案是：﹣ ．
【考點精析】本題主要考查了函數奇偶性的性質的相關知識點，需要掌握在公共定義域內，偶函數的加減乘除仍為偶函數；奇函數的加減仍為奇函數；奇數個奇函數的乘除認為奇函數；偶數個奇函數的乘除為偶函數；一奇一偶的乘積是奇函數;復合函數的奇偶性：一個為偶就為偶，兩個為奇才為奇才能正確解答此題．
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，橢圓
的離心率為
，過橢圓右焦點
作兩條互相垂直的弦
與
．當直線斜率為0時，
．
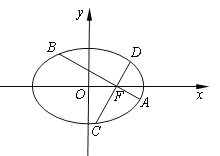
（1）求橢圓的方程；
（2）求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國古代數學名著《算法統宗》中有如下問題：“遠望巍巍塔七層，紅光點點倍加增，共燈三百八十一，請問尖頭幾盞燈？”意思是：一座7層塔共掛了381盞燈，且相鄰兩層中的下一層燈數是上一層燈數的2倍，則塔的頂層共有燈（ ）
A.1盞
B.3盞
C.5盞
D.9盞
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P﹣ABCD中，側面PAD為等邊三角形且垂直于底面ABCD，AB=BC= 
AD，∠BAD=∠ABC=90°，E是PD的中點．
（Ⅰ）證明：直線CE∥平面PAB；
（Ⅱ）點M在棱PC 上，且直線BM與底面ABCD所成角為45°，求二面角M﹣AB﹣D的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和為Sn ， 已知S2=6，an+1=4Sn+1，n∈N* ．
（1）求通項an；
（2）設bn=an﹣n﹣4，求數列{|bn|}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解市民對某項政策的態度，隨機抽取了男性市民25人，女性市民75人進行調查，得到以下的
列聯表：
支持 | 不支持 | 合計 | |
男性 | 20 | 5 | 25 |
女性 | 40 | 35 | 75 |
合計 | 60 | 40 | 100 |
根據以上數據，能否有97.5%的把握認為市民“支持政策”與“性別”有關？
將上述調查所得的頻率視為概率，現在從所有市民中，采用隨機抽樣的方法抽取4位市民進行長期跟蹤調查，記被抽取的4位市民中持“支持”態度的人數為X,求X的分布列及數學期望。
附：
.
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ln（x﹣1）﹣kx+k+1．
（1）當k=1時，證明：f（x）≤0；
（2）求函數f（x）的單調區間；
（3）證明： 
+ 
+…+ 
＜ 
（n∈N* ， 且n≥2）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數f（x）=Asin（ωx+φ）滿足：f（ 
+x）=﹣f（ ﹣x），且f（ 
+x）=f（ ﹣x），則ω的一個可能取值是（ ）
A.2
B.3
C.4
D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
