
【題目】我國古代數(shù)學名著《算法統(tǒng)宗》中有如下問題:“遠望巍巍塔七層,紅光點點倍加增,共燈三百八十一,請問尖頭幾盞燈?”意思是:一座7層塔共掛了381盞燈,且相鄰兩層中的下一層燈數(shù)是上一層燈數(shù)的2倍,則塔的頂層共有燈( )
A.1盞
B.3盞
C.5盞
D.9盞
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù) ![]() (其中ω>0),若f(x)的一條對稱軸離最近的對稱中心的距離為
(其中ω>0),若f(x)的一條對稱軸離最近的對稱中心的距離為 ![]() .
.
(1)求y=f(x)的單調遞增區(qū)間;
(2)在△ABC中角A、B、C的對邊分別是a,b,c滿足(2b﹣a)cosC=ccosA,則f(B)恰是f(x)的最大值,試判斷△ABC的形狀.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知拋物線x2=y,點A(﹣ ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),拋物線上的點P(x,y)(﹣
),拋物線上的點P(x,y)(﹣ ![]() <x<
<x< ![]() ),過點B作直線AP的垂線,垂足為Q.
),過點B作直線AP的垂線,垂足為Q.
(Ⅰ)求直線AP斜率的取值范圍;
(Ⅱ)求|PA||PQ|的最大值.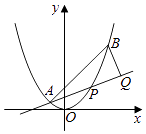
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某公司為確定下一年度投人某種產品的宣傳費,需了解年宣傳費![]() 對年銷售額(單位:萬元)的影響,對近6年的年宣傳費
對年銷售額(單位:萬元)的影響,對近6年的年宣傳費![]() 和年銷售額
和年銷售額![]() 數(shù)據(jù)進行了研究,發(fā)現(xiàn)宣傳費
數(shù)據(jù)進行了研究,發(fā)現(xiàn)宣傳費![]() 和年銷售額
和年銷售額![]() 具有線性相關關系,并對數(shù)據(jù)作了初步處理,得到下面的一些統(tǒng)計量的值.
具有線性相關關系,并對數(shù)據(jù)作了初步處理,得到下面的一些統(tǒng)計量的值.

(I)根據(jù)表中數(shù)據(jù)建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(Ⅱ)利用(I)中的回歸方程預測該公司如果對該產品的宜傳費支出為10萬元時銷售額是![]() 萬元,該公司計劃從10名中層管理人員中挑選3人擔任總裁助理,10名中層管理人員中有2名是技術部骨干,記所挑選3人中技術部骨干人數(shù)為
萬元,該公司計劃從10名中層管理人員中挑選3人擔任總裁助理,10名中層管理人員中有2名是技術部骨干,記所挑選3人中技術部骨干人數(shù)為![]() 且隨機變量
且隨機變量![]() ,求
,求![]() 的概率分布列與數(shù)學期望.
的概率分布列與數(shù)學期望.
附:回歸直線的傾斜率截距的最小二乘估計公式分別為:
 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知{an}為等差數(shù)列,前n項和為Sn(n∈N+),{bn}是首項為2的等比數(shù)列,且公比大于0,b2+b3=12,b3=a4﹣2a1 , S11=11b4 .
(Ⅰ)求{an}和{bn}的通項公式;
(Ⅱ)求數(shù)列{a2nb2n﹣1}的前n項和(n∈N+).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
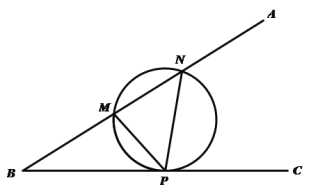
【題目】米勒問題,是指德國數(shù)學家米勒1471年向諾德爾教授提出的有趣問題:在地球表面的什么部位,一根垂直的懸桿呈現(xiàn)最長(即可見角最大?)米勒問題的數(shù)學模型如下:如圖,設![]() 是銳角
是銳角![]() 的一邊
的一邊![]() 上的兩定點,點
上的兩定點,點![]() 是邊
是邊![]() 邊上的一動點,則當且僅當
邊上的一動點,則當且僅當![]() 的外接圓與邊
的外接圓與邊![]() 相切時,
相切時,![]() 最大.若
最大.若![]() ,點
,點![]() 在
在![]() 軸上,則當
軸上,則當![]() 最大時,點
最大時,點![]() 的坐標為( )
的坐標為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)利用“五點法”畫出函數(shù)![]() 在一個周期
在一個周期![]() 上的簡圖;
上的簡圖;
(2)先把![]() 的圖象上所有點向左平移
的圖象上所有點向左平移![]() 個單位長度,得到
個單位長度,得到![]() 的圖象;然后把
的圖象;然后把![]() 的圖
的圖
象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),得到![]() 的圖象;再把
的圖象;再把![]() 的圖象
的圖象
上所有點的縱坐標縮短到原來的![]() 倍(橫坐標不變),得到
倍(橫坐標不變),得到![]() 的圖象,求
的圖象,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】盒中裝有![]() 個零件,其中
個零件,其中![]() 個是使用過的,另外
個是使用過的,另外![]() 個未經使用.
個未經使用.
(1)從盒中每次隨機抽取![]() 個零件,每次觀察后都將零件放回盒中,求
個零件,每次觀察后都將零件放回盒中,求![]() 次抽取中恰有
次抽取中恰有![]() 次抽到使用過的零件的概率;
次抽到使用過的零件的概率;
(2)從盒中隨機抽取![]() 個零件,使用后放回盒中,記此時盒中使用過的零件個數(shù)為
個零件,使用后放回盒中,記此時盒中使用過的零件個數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com