
【題目】已知函數(shù)![]() .
.
(1)判斷![]() 的單調(diào)性;
的單調(diào)性;
(2)已知![]() :不等式
:不等式![]() 對任意
對任意![]() 恒成立;
恒成立;![]() :函數(shù)
:函數(shù)![]() 的兩個零點分別在區(qū)間
的兩個零點分別在區(qū)間![]() 和
和![]() 內(nèi),如果
內(nèi),如果![]() 為真,
為真,![]() 為假,求實數(shù)
為假,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)當(dāng)![]() ,且
,且![]() 時,
時,![]() 單調(diào)遞增;(2)
單調(diào)遞增;(2)![]() .
.
【解析】
試題分析:(1)由題意可利用分類討論法進(jìn)行求解,當(dāng)![]() 時,有
時,有![]() ,且
,且![]() 為增函數(shù),
為增函數(shù),![]() 為減函數(shù),從而
為減函數(shù),從而![]() 為增函數(shù),所以
為增函數(shù),所以![]() 為增函數(shù),當(dāng)
為增函數(shù),當(dāng)![]() 時,
時,![]() ,且
,且![]() 為減函數(shù),
為減函數(shù),![]() 為增函數(shù),從而
為增函數(shù),從而![]() 為減函數(shù),所以
為減函數(shù),所以![]() 為增函數(shù),故當(dāng)
為增函數(shù),故當(dāng)![]() ,且
,且![]() 時,
時,![]() 單調(diào)遞增;(2)由(1)知
單調(diào)遞增;(2)由(1)知![]() 在
在![]() 上是增函數(shù),則
上是增函數(shù),則![]() 在
在![]() 上的最大值為
上的最大值為![]() ,若不等式
,若不等式![]() 對任意
對任意![]() 恒成立,則
恒成立,則![]() ;若函數(shù)
;若函數(shù)![]() 的兩個零點分別在區(qū)間
的兩個零點分別在區(qū)間![]() 和
和![]() 內(nèi),由二分法可得
內(nèi),由二分法可得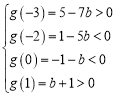 ,得
,得![]() .又因為
.又因為![]() 為真,
為真,![]() 為假,所以
為假,所以![]() 、
、![]() 一真一假,若
一真一假,若![]() 真,
真,![]() 假,則有
假,則有![]() ;若
;若![]() 假,
假,![]() 真,則
真,則![]() .故實數(shù)
.故實數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:(1)當(dāng)![]() 時,
時,![]() 為增函數(shù),
為增函數(shù),![]() 為減函數(shù),
為減函數(shù),
從而![]() 為增函數(shù),所以
為增函數(shù),所以![]() 為增函數(shù),
為增函數(shù),
當(dāng)![]() 時,
時,![]() ,
,
![]() 為減函數(shù),
為減函數(shù),![]() 為增函數(shù),
為增函數(shù),
從而![]() 為減函數(shù),所以
為減函數(shù),所以![]() 為增函數(shù),
為增函數(shù),
故當(dāng)![]() ,且
,且![]() 時,
時,![]() 單調(diào)遞增.……………………………………5分
單調(diào)遞增.……………………………………5分
(2)由(1)知![]() 在
在![]() 上是增函數(shù),則
上是增函數(shù),則
![]() 在
在![]() 上的最大值為
上的最大值為![]() ,
,
若不等式![]() 對任意
對任意![]() 恒成立,則
恒成立,則![]() .……………………7分
.……………………7分
若函數(shù)![]() 的兩個零點分別在區(qū)間
的兩個零點分別在區(qū)間![]() 和
和![]() 內(nèi),
內(nèi),
則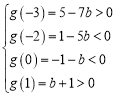 ,得
,得![]() .……………………………………9分
.……………………………………9分
∵![]() 為真,
為真,![]() 為假,∴
為假,∴![]() 、
、![]() 一真一假,
一真一假,
若![]() 真,
真,![]() 假,則有
假,則有![]() ;若
;若![]() 假,
假,![]() 真,則
真,則![]() .
.
故實數(shù)![]() 的取值范圍是
的取值范圍是![]() .…………………………12分
.…………………………12分


 步步高達(dá)標(biāo)卷系列答案
步步高達(dá)標(biāo)卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
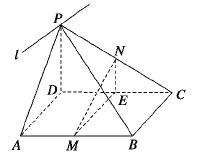
【題目】如圖,P為平行四邊形ABCD所在平面外一點,MN分別為ABPC的中點,平面PAD∩平面PBC=l.
(1)判斷BC與l的位置關(guān)系,并證明你的結(jié)論;
(2)判斷MN與平面PAD的位置關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一點,
上的一點,![]() 分別為
分別為![]() 的中點.
的中點.

(1)求證:![]() ∥平面
∥平面![]() ;
;
(2)當(dāng)![]() 為
為![]() 的中點時,求三棱錐
的中點時,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分別為角A,B,C的對邊,在四面體PABC中,S1,S2,S3,S分別表示△PAB,△PBC,△PCA,△ABC的面積,α,β,γ依次表示面PAB,面PBC,面PCA與底面ABC所成二面角的大小.寫出對四面體性質(zhì)的猜想,并證明你的結(jié)論


查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知甲、乙兩煤礦每年的產(chǎn)量分別為200萬噸和300萬噸,需經(jīng)過東車站和西車站兩個車站運往外地,東車站每年最多能運280萬噸煤,西車站每年最多能運360萬噸煤,甲煤礦運往東車站和西車站的運費價格分別為1元/噸和1.5元/噸,乙煤礦運往東車站和西車站的運費價格分別為0.8元/噸和1.6元/噸.要使總運費最少,煤礦應(yīng)怎樣編制調(diào)運方案?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)共有20條生產(chǎn)線,由于受生產(chǎn)能力和技術(shù)水平等因素的影響,會產(chǎn)生一定量的次品.根據(jù)經(jīng)驗知道,每臺機器產(chǎn)生的次品數(shù)![]() 萬件與每臺機器的日產(chǎn)量
萬件與每臺機器的日產(chǎn)量![]() 萬件
萬件![]() 之間滿足關(guān)系:
之間滿足關(guān)系:![]() .已知每生產(chǎn)1萬件合格的產(chǎn)品可以以盈利3萬元,但每生產(chǎn)1萬件次品將虧損1萬元.
.已知每生產(chǎn)1萬件合格的產(chǎn)品可以以盈利3萬元,但每生產(chǎn)1萬件次品將虧損1萬元.
(Ⅰ)試將該企業(yè)每天生產(chǎn)這種產(chǎn)品所獲得的利潤![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(Ⅱ)當(dāng)每臺機器的日產(chǎn)量為多少時,該企業(yè)的利潤最大,最大為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),
為參數(shù),![]() ),在以坐標(biāo)原點為極點,
),在以坐標(biāo)原點為極點,![]() 軸正半軸為極軸的極坐標(biāo)系中,曲線
軸正半軸為極軸的極坐標(biāo)系中,曲線![]() .
.
(1)求曲線![]() 的普通方程,并將
的普通方程,并將![]() 的方程化為極坐標(biāo)方程;
的方程化為極坐標(biāo)方程;
(2)直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,其中
,其中![]() 滿足
滿足![]() ,若曲線
,若曲線![]() 與
與![]() 的公共點都在
的公共點都在![]() 上,求
上,求![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com