日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
設z1=1-cosθ＋isinθ，z2=a2＋ai(a∈R).若z1·z2是純虛數，問在(0，2π)內是否存在θ使(z1-z2)2是實數？

解：假設存在滿足條件的θ，則由z1·z2為純虛數可得

由上可知a≠0，cosθ≠1,∴a=

要使(z1-z2)2是實數，就是要(z1-z2)是實數或為純虛數.

但是z1-z2=(1-cosθ-a2)＋(sinθ-a)i.

∴sinθ-a=0或1-cosθ-a2=0.

由

都可解得θ=或θ=.

故滿足條件的θ存在.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設z1=1-cosθ+isinθ，z2=a2+ai（a∈R），若z1z2≠0，z1z2-
.
z1z2
=0，問在（0，2π）內是否存在θ使（z1-z2）2為實數？若存在，求出θ的值；若不存在，請說明理由．

查看答案和解析>>

科目：高中數學 來源： 題型：

設z1=1-cosθ+isinθ,z2=()2+i,問在(0,2π)內是否存在θ,

       (1)使z1-z2為實數?

       (2)使z1-z2為純虛數?

      

查看答案和解析>>

科目：高中數學 來源： 題型：閱讀理解

(本題14分)閱讀：設Z點的坐標(a, b)，r=||，θ是以x軸的非負半軸為始邊、以OZ所在的射線為終邊的角，復數z=a+bi還可以表示為z=r(cosθ+isinθ)，這個表達式叫做復數z的三角形式，其中，r叫做復數z的模，當r≠0時，θ叫做復數z的幅角，復數0的幅角是任意的，當0≤θ<2π時，θ叫做復數z的幅角主值，記作argz．

根據上面所給出的概念，請解決以下問題：

(1)設z=a+bi =r(cosθ+isinθ) (a、bÎR，r≥0)，請寫出復數的三角形式與代數形式相互之間的轉換關系式；

(2)設z1=r1(cosθ1+isinθ1)，z2=r2(cosθ2+isinθ2)，探索三角形式下的復數乘法、除法的運算法則，請寫出三角形式下的復數乘法、除法的運算法則．(結論不需要證明)

查看答案和解析>>

科目：高中數學 來源：高考數學一輪復習必備（第104-106課時）：第十四章 復數-復數的有關概念（解析版） 題型：解答題

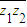設z1=1-cosθ+isinθ，z2=a2+ai（a∈R），若z1z2≠0，z1z2-=0，問在（0，2π）內是否存在θ使（z1-z2）2為實數？若存在，求出θ的值；若不存在，請說明理由．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 一区二区三区精品视频 | 两性免费视频 | 欧美精品一区二区三区一线天视频 | 亚洲品质自拍视频网站 | 91精品国产麻豆 | 成人亚洲精品 | 91视频免费播放 | 太子妃好紧皇上好爽h | 直接看av的网站 | 天天干一干 | 美女视频黄色 | 亚洲成人一区二区三区 | 国产日韩一区二区 | 午夜精品成人一区二区 | 久久亚洲一区 | 一级毛片在线播放 | 国产一区精品在线 | 中文字幕高清 | 久久国产欧美日韩精品 | 国产午夜视频 | 日韩精品在线观看一区 | 三级免费黄 | 色呦呦| 黄色免费看网站 | 欧美1区2区3区 | 午夜免费| 亚洲精品一区二三区不卡 | 妞干网福利视频 | 欧美国产精品一区 | 最新黄网在线观看 | 激情视频一区二区三区 | 久久精品视频亚洲 | 日韩视频免费在线 | 日韩中文字幕在线看 | 后进极品白嫩翘臀在线视频 | 国产精品无码久久久久 | 日韩一区二区三区在线视频 | 国产一区二区三区久久 | 日韩成人在线免费观看 | 国产免费观看一区二区三区 | 色婷婷中文 |