
【題目】已知點![]() ,拋物線
,拋物線![]() :
:![]() 的焦點為
的焦點為![]() ,射線
,射線![]() 與拋物線
與拋物線![]() 相交于點
相交于點![]() ,與其準線相交于點
,與其準線相交于點![]() ,則
,則![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
求出拋物線C的焦點F的坐標,從而得到AF的斜率k=-2.過M作MP⊥l于P,根據拋物線物定義得|FM|=|PM|.Rt△MPN中,根據tan∠NMP=﹣k=2,從而得到|PN|=2|PM|,進而算出|MN|![]() |PM|,由此即可得到|FM|:|MN|的值.
|PM|,由此即可得到|FM|:|MN|的值.
∵拋物線C:y2=4x的焦點為F(1,0),點A坐標為(0,2),
∴拋物線的準線方程為l:x=﹣1,直線AF的斜率為k=﹣2,
過M作MP⊥l于P,根據拋物線物定義得|FM|=|PM|,
∵Rt△MPN中,tan∠NMP=﹣k=2,
∴![]() 2,可得|PN|=2|PM|,
2,可得|PN|=2|PM|,
得|MN|![]() |PM|,
|PM|,
因此可得|FM|:|MN|=|PM|:|MN|=1:![]() .
.
故選:C.


科目:高中數學 來源: 題型:
【題目】關于函數![]() 有如下命題:
有如下命題:
①![]() ; ②函數的圖象關于原點中心對稱;
; ②函數的圖象關于原點中心對稱;
③函數的定義域與值域相同; ④函數的圖象必經過第二、四象限.
其中正確命題的個數是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的離心率為
)的離心率為![]() ,短軸端點到焦點的距離為
,短軸端點到焦點的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() ,
,![]() 為橢圓
為橢圓![]() 上任意兩點,
上任意兩點,![]() 為坐標原點,且
為坐標原點,且![]() .求證:原點
.求證:原點![]() 到直線
到直線![]() 的距離為定值,并求出該定值.
的距離為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年是某市大力推進居民生活垃圾分類的關鍵一年,有關部門為宣傳垃圾分類知識,面向該市市民進行了一次“垃圾分類知識”的網絡問卷調查,每位市民僅有一次參與機會,通過抽樣,得到參與問卷調查中的1000人的得分數據,其頻率分布直方圖如圖所示:
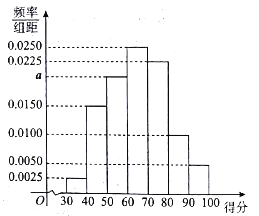
(1)估計該組數據的中位數、眾數;
(2)由頻率分布直方圖可以認為,此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
, ![]() 近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表),利用該正態分布,求
近似為這1000人得分的平均值(同一組數據用該區間的中點值作代表),利用該正態分布,求![]() ;
;
(3)在(2)的條件下,有關部門為此次參加問卷調查的市民制定如下獎勵方案:
(ⅰ)得分不低于![]() 可獲贈2次隨機話費,得分低于
可獲贈2次隨機話費,得分低于![]() 則只有1次;
則只有1次;
(ⅱ)每次贈送的隨機話費和對應概率如下:

現有一位市民要參加此次問卷調查,記![]() (單位:元)為該市民參加問卷調查獲贈的話費,求
(單位:元)為該市民參加問卷調查獲贈的話費,求![]() 的分布列和數學期望.
的分布列和數學期望.
附: ![]() ,
,
若![]() ,則
,則![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2ex+3x2-2x+1+b,x∈R的圖象在x=0處的切線方程為y=ax+2.
(1)求函數f(x)的單調區間與極值;
(2)若存在實數x,使得f(x)-2x2-3x-2-2k≤0成立,求整數k的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com