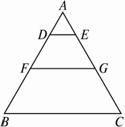
圖1-3-14
思路分析:要求題目中的三部分的面積比，必須先求出△ADE、△AFG和△ABC的面積，才能求出兩個四邊形的面積.由已知DE∥FG∥BC的條件，可以得到相似三角形，再由相似三角形的面積比等于相似比的平方的性質，可求出相似三角形的面積比.題目中未給出具體數值，故應引入參數.
解：∵AD∶DF∶FB =2∶3∶4，?
設AD =2k,DF =3k,FB =4k(k＞0)，則AF =5k,AB =9k.?
∵DE∥FG,∴△ADE∽△AFG.?
∴
=(
)2=(
)2=
.?
同理,可得
=(
)2=
.
設S△ADE =4a,則S△AFG?=25a,S△ABC =81a(a＞0).?
∴S四邊形DEGF =25a - 4a =21a，?
S四邊形BCGF?=81a - 25a = 56a.?
∴S△ADE∶S四邊形DEGF∶S四邊形BCGF=4∶21∶56.
科目：高中數學 來源： 題型：
（本小題滿分14分）如圖9-3，已知：射線OA為y=kx(k>0，x>0)，射線OB為y= －kx(x>0)，動點P(x，y)在∠AOx的內部，PM⊥OA于M，PN⊥OB于N，四邊形ONPM的面積恰為k.
（1）當k為定值時，動點P的縱坐標y是橫坐標x的函數，求這個函數y=f(x)的解析式；
（2）根據k的取值范圍，確定y=f(x)的定義域.
查看答案和解析>>
科目：高中數學 來源：2012-2013學年廣東省揭陽市高三3月第一次高考模擬理科數學試卷（解析版） 題型：解答題
（本小題滿分14分）
如圖1，在等腰梯形CDEF中，CB、DA是梯形的高，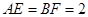
，
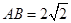,現將梯形沿CB、DA折起，使
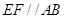且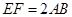
，得一簡單組合體
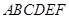如圖2示，已知
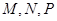分別為
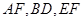的中點．
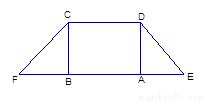
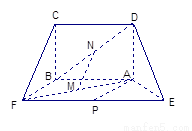
圖1 圖2
（1）求證：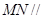
平面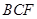
；
（2）求證：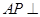
；
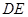（3）當
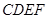多長時，平面
與平面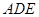
所成的銳二面角為
？
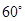查看答案和解析>>
科目：高中數學 來源： 題型：
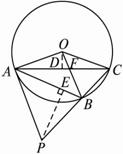
圖2-3-14
(1)求弦AC、AB的長;
(2)若P為CB延長線上的一點,試確定P點的位置,使得PA與⊙O相切,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
