
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,側(cè)棱
是正方形,側(cè)棱![]() 底面
底面![]() 是
是![]() 中點(diǎn),
中點(diǎn),
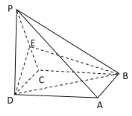
(1)證明:![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() .
.
【答案】(1)證明見解析;(2)證明見解析.
【解析】
試題分析:(1)連結(jié)![]() ,設(shè)
,設(shè)![]() 與
與![]() 交于
交于![]() 點(diǎn),連結(jié)
點(diǎn),連結(jié)![]() ,易證
,易證![]() 為
為![]() 的中位線,從而
的中位線,從而![]() ,再利用線面平行的判斷定理即可證得
,再利用線面平行的判斷定理即可證得![]() 平面
平面![]() ;(2)依題意,易證
;(2)依題意,易證![]() 底面
底面![]() ,再利用面面垂直的判斷定理即可證得平面
,再利用面面垂直的判斷定理即可證得平面![]() 平面
平面![]() .
.
試題解析:(1)連接![]() 交
交![]() 于
于![]() ,連接
,連接![]()
∵底面![]() 是正方形,∴
是正方形,∴![]() 為
為![]() 中點(diǎn),∵在
中點(diǎn),∵在![]() 中,
中,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),
∴![]() …………(3分)
…………(3分)
∵![]() 平面
平面![]() 平面
平面![]() ,∴在
,∴在![]() 平面
平面![]() …………(5分)
…………(5分)
(2)∵側(cè)棱![]() 底面
底面![]() 底面
底面![]() ,∴
,∴![]()
∵底面![]() 是正方形,∴
是正方形,∴![]()
∵![]() 與
與![]() 為平面
為平面![]() 內(nèi)兩條相交直線,∴
內(nèi)兩條相交直線,∴![]() 平面
平面![]() …………(8分)
…………(8分)
∵![]() 平面
平面![]() ,∴
,∴![]()
∵![]() 是
是![]() 的中點(diǎn),∴
的中點(diǎn),∴![]()
∵![]() 與
與![]() 為平面
為平面![]() 內(nèi)兩條相交直線,∴
內(nèi)兩條相交直線,∴![]() 平面
平面![]() …………(11分)
…………(11分)
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() …………(12分)
…………(12分)


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】微信是騰訊公司推出的一種手機(jī)通訊軟件,它支持發(fā)送語音短信、視頻、圖片和文字,一經(jīng)推出便風(fēng)靡全國,甚至涌現(xiàn)出一批在微信的朋友圈內(nèi)銷售商品的人(被稱為微商).為了調(diào)查每天微信用戶使用微信的時(shí)間,某經(jīng)銷化妝品的微商在一廣場(chǎng)隨機(jī)采訪男性、女性用戶各50名,其中每天玩微信超過6小時(shí)的用戶列為“微信控”,否則稱其為“非微信控”,調(diào)查結(jié)果如下:
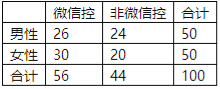
(1)根據(jù)以上數(shù)據(jù),能否有60%的把握認(rèn)為“微信控”與”性別“有關(guān)?
(2)現(xiàn)從調(diào)查的女性用戶中按分層抽樣的方法選出5人贈(zèng)送營養(yǎng)面膜1份,求所抽取5人中“微信控”和“非微信控”的人數(shù);
(3)從(2)中抽取的5人中再隨機(jī)抽取3人贈(zèng)送200元的護(hù)膚品套裝,記這3人中“微信控”的人數(shù)為X,試求X的分布列與數(shù)學(xué)期望.
參考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
參考數(shù)據(jù):

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),△
的中點(diǎn),△![]() 是等腰三角形,
是等腰三角形,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 上一點(diǎn).
上一點(diǎn).

(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 將三棱柱
將三棱柱![]() 分成兩個(gè)部分,求較小部分與較大部分的體積之比.
分成兩個(gè)部分,求較小部分與較大部分的體積之比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】心理學(xué)家分析發(fā)現(xiàn)視覺和空間能力與性別有關(guān),某數(shù)學(xué)興趣小組為了驗(yàn)證這個(gè)結(jié)論,從興趣小組中按分層抽樣的方法抽取50名同學(xué)(男30女20),給所有同學(xué)幾何題和代數(shù)題各一題,讓各位同學(xué)自由選擇一道題進(jìn)行解答.選題情況如下表:(單位:人)

(Ⅰ)能否據(jù)此判斷有97.5%的把握認(rèn)為視覺和空間能力與性別有關(guān)?
(Ⅱ)經(jīng)過多次測(cè)試后,甲每次解答一道幾何題所用的時(shí)間在5—7分鐘,乙每次解答一道幾何題所用的時(shí)間在6—8分鐘,現(xiàn)甲、乙各解同一道幾何題,求乙比甲先解答完的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直角△![]() 如圖所示,其中
如圖所示,其中![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 邊上的中點(diǎn).現(xiàn)沿折痕
邊上的中點(diǎn).現(xiàn)沿折痕![]()
![]() 將
將![]() 翻折,使得
翻折,使得![]() 與平面
與平面![]() 外一點(diǎn)
外一點(diǎn)![]() 重合,得到如圖(2)所示的幾何體.
重合,得到如圖(2)所示的幾何體.


(1)證明:平面![]() 平面
平面![]() ;
;
(2)記平面![]() 與平面
與平面![]() 的交線為
的交線為![]() ,探究:直線
,探究:直線![]() 與
與![]() 是否平行.若平行,請(qǐng)給出證明,若不平行,請(qǐng)說明理由.
是否平行.若平行,請(qǐng)給出證明,若不平行,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直四棱柱ABCD-A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分別是棱AD,AA1的中點(diǎn).

(1)設(shè)F是棱AB的中點(diǎn),證明:直線EE1∥平面FCC1;
(2)證明:平面D1AC⊥平面BB1C1C;
(3)求點(diǎn)D到平面D1AC的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)記![]() ,判斷
,判斷![]() 在區(qū)間
在區(qū)間![]() 內(nèi)的零點(diǎn)個(gè)數(shù)并說明理由;
內(nèi)的零點(diǎn)個(gè)數(shù)并說明理由;
(2)記![]() 在
在![]() 內(nèi)的零點(diǎn)為
內(nèi)的零點(diǎn)為![]() ,
,![]() ,若
,若![]() (
(![]() )在
)在![]() 內(nèi)有兩個(gè)不等實(shí)根
內(nèi)有兩個(gè)不等實(shí)根![]() ,
,![]() (
(![]() ),判斷
),判斷![]() 與
與![]() 的大小,并給出對(duì)應(yīng)的證明.
的大小,并給出對(duì)應(yīng)的證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 為常數(shù).
為常數(shù).
(1)若曲數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與直線
處的切線與直線![]() 垂直,求函數(shù)
垂直,求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(2)若函數(shù)![]() 在區(qū)間[1,3]上的最小值為
在區(qū)間[1,3]上的最小值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某城區(qū)有農(nóng)民、工人、知識(shí)分子家庭共計(jì)2 007戶,其中農(nóng)民家庭1 600戶,工人家庭304戶.現(xiàn)要從中抽取容量為40的樣本,則在整個(gè)抽樣過程中,可以用到下列抽樣方法中的( )
①簡單隨機(jī)抽樣 ②系統(tǒng)抽樣 ③分層抽樣
A. ②③ B. ①③
C. ③ D. ①②③
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com