如圖1：等邊
可以看作由等邊
繞頂點(diǎn)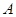
經(jīng)過旋轉(zhuǎn)相似變換得到.但是我們注意到圖形中的
和
的關(guān)系，上述變換也可以理解為圖形是由繞頂點(diǎn)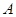旋轉(zhuǎn)
形成的.于是我們得到一個結(jié)論：如果兩個正三角形存在著公共頂點(diǎn)，則該圖形可以看成是由一個三角形繞著該頂點(diǎn)旋轉(zhuǎn)形成的.
① 利用上述結(jié)論解決問題：如圖2，中，
都是等邊三角形，求四邊形
的面積;
② 圖3中, ∽，
，仿照上述結(jié)論,推廣出符合圖3的結(jié)論.（寫出結(jié)論即可）
應(yīng)用題天天練四川大學(xué)出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源：2010-2011年安徽省蚌埠市七中高一自主招生考試數(shù)學(xué) 題型：解答題
如圖1：等邊
可以看作由等邊
繞頂點(diǎn)
經(jīng)過旋轉(zhuǎn)相似變換得到.但是我們注意到圖形中的
和
的關(guān)系，上述變換也可以理解為圖形是由繞頂點(diǎn)旋轉(zhuǎn)
形成的.于是我們得到一個結(jié)論：如果兩個正三角形存在著公共頂點(diǎn)，則該圖形可以看成是由一個三角形繞著該頂點(diǎn)旋轉(zhuǎn)形成的.
① 利用上述結(jié)論解決問題：如圖2，中，
都是等邊三角形，求四邊形
的面積;
② 圖3中, ∽，
，仿照上述結(jié)論,推廣出符合圖3的結(jié)論.（寫出結(jié)論即可）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
如圖，在邊長為1個單位長度的小正方形組成的網(wǎng)格中，給出了格點(diǎn)△ABC（頂點(diǎn)是網(wǎng)格線的交點(diǎn)）和點(diǎn)A1.
（1）畫出一個格點(diǎn)△A1B1C1，
并使它與△ABC全等且A與A1是對應(yīng)點(diǎn)；
（2）畫出點(diǎn)B關(guān)于直線AC的對稱點(diǎn)D，并指出AD可以看作由AB繞A點(diǎn)經(jīng)過怎樣的旋轉(zhuǎn)而得到的.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，則該圖形可以看成一個三角形繞著該頂點(diǎn)旋轉(zhuǎn)