【題目】設橢圓
的焦點分別為
、
，直線
：
交
軸于點
，且
（1）求橢圓的方程；
（2）過
分別作互相垂直的兩直線
，與橢圓分別交于D、E和M、N四點， 求四邊形
面積的最大值和最小值．
科目：高中數學 來源： 題型：
【題目】為了培養學生的安全意識，某中學舉行了一次“安全自救”的知識競賽活動，共有800名學生參加了這次競賽.為了解本次競賽的成績情況，從中抽取了部分學生的成績（得分均為整數，滿分為100分）進行統計，得到如下的頻率分布表，請你根據頻率分布表解答下列問題：
序號（i） | 分組（分數） | 組中值（Gi） | 頻數（人數） | 頻率（fi） |
1 |
| 65 | ① | 0.10 |
2 |
| 75 | 20 | ② |
3 |
| 85 | ③ | 0.20 |
4 |
| 95 | ④ | ⑤ |
合計 | 50 | 1.00 | ||
（1）求出頻率分布表中①②③④⑤處的值；
（2）為鼓勵更多的學生了解“安全自救”知識，成績不低于85分的學生能獲獎，請估計在參加的800名學生中大約有多少名學生能獲獎；
（3）求這800名學生的平均分.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的兩個焦點坐標分別是
、
，并且經過點
.
（1）求橢圓
的方程；
（2）若直線
與圓
：
相切，并與橢圓交于不同的兩點
、
.當
，且滿足
時，求
面積
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若實數
滿足
，稱為函數
的不動點.有下面三個命題：（1）若是二次函數，且沒有不動點，則函數
也沒有不動點；（2）若是二次函數，則函數可能有
個不動點；（3）若的不動點的個數是
，則的不動點的個數不可能是
；它們中所有真命題的序號是________________________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在《爸爸去哪兒》第二季第四期中，村長給6位“萌娃”布置一項搜尋空投食物的任務.已知：①食物投擲地點有遠、近兩處；②由于Grace年紀尚小，所以要么不參與該項任務，但此時另需一位小孩在大本營陪同，要么參與搜尋近處投擲點的食物；③所有參與搜尋任務的小孩須被均分成兩組，一組去遠處，一組去近處，那么不同的搜尋方案有______種.（以數字作答）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對定義在
上的函數
和常數
，
，若
恒成立，則稱
為函數的一個“凱森數對”.
（1）若
是的一個“凱森數對”，且
，求
；
（2）已知函數
與
的定義域都為，問它們是否存在“凱森數對”？分別給出判斷并說明理由；
（3）若
是的一個“凱森數對”，且當
時，
，求在區間
上的不動點個數（函數
的不動點即為方程
的解）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C過點M（0，-2）、N（3，1），且圓心C在直線x+2y+1=0上．
（1）求圓C的方程；
（2）設直線ax-y+1=0與圓C交于A，B兩點，是否存在實數a，使得過點P（2，0）的直線l垂直平分弦AB？若存在，求出實數a的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】歐拉公式
（
為虛數單位，
，
為自然底數）是由瑞士著名數學家歐拉發明的，它將指數函數的定義域擴大到復數，建立了三角函數和指數函數的關系，它在復變函數論里占有非重要的地位，被譽為“數學中的天橋”，根據歐拉公式可知，
表示的復數在復平面中位于（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數學是研究數量、結構、變化、空間以及信息等概念的一門科學.在人類歷史發展和社會生活中，數學發揮著不可替代的作用，也是學習和研究現代科學技術必不可少的基本工具.
（1）為調查大學生喜歡數學命題是否與性別有關，隨機選取
名大學生進行問卷調查，當被調查者問卷評分不低于
分則認為其喜歡數學命題，當評分低于分則認為其不喜歡數學命題，問卷評分的莖葉圖如下：
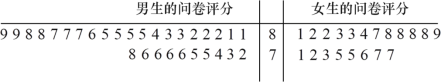
依據上述數據制成如下列聯表：
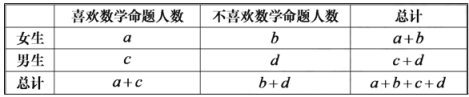
請問是否有
的把握認為大學生是否喜歡數學命題與性別有關？
參考公式及數據：
.
|
|
|
|
|
|
|
|
|
|
（2）在某次命題大賽中，
同學要進行
輪命題，其在每輪命題成功的概率均為
，各輪命題相互獨立，若該同學在
輪命題中恰有
次成功的概率為
，記該同學在輪命題中的成功次數為
，求
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
