
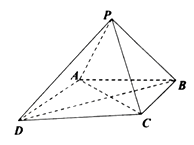
【題目】如圖,在四棱錐 ![]() 中,
中, ![]() 、
、 ![]() 、
、 ![]() 均為等邊三角形,
均為等邊三角形, ![]() .
.
(Ⅰ)求證: ![]() 平面
平面 ![]() ;
;
(Ⅱ)求直線 ![]() 與平面
與平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】解:(Ⅰ)因為 ![]() ,
, ![]() ,
, ![]() 為公共邊,
為公共邊,
所以 ![]() ,
,
所以 ![]() ,又
,又 ![]() ,
,
所以 ![]() ,且
,且 ![]() 為
為 ![]() 中點.
中點.
又 ![]() ,所以
,所以 ![]() ,
,
又 ![]() ,所以
,所以 ![]() ,結合
,結合 ![]() ,
,
可得 ![]() ,
,
所以 ![]() ,
,
即 ![]() ,又
,又 ![]() ,
,
故 ![]() 平面
平面 ![]() ,又
,又 ![]() 平面
平面 ![]() ,所以
,所以 ![]() .
.
又 ![]() ,所以
,所以 ![]() 平面
平面 ![]() .
.
(Ⅱ)以 ![]() 為原點,建立空間直角坐標系
為原點,建立空間直角坐標系 ![]() 如圖所示,
如圖所示,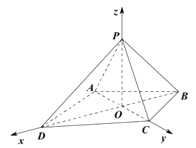
不妨設 ![]() ,易得
,易得 ![]() ,
, ![]() ,
,
則 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以 ![]() ,
, ![]() ,
, ![]() ,
,
設平面 ![]() 的法向量為
的法向量為 ![]() ,則
,則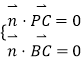 ,即
,即 ![]() ,解得
,解得 ![]() ,
,
令 ![]() 得
得 ![]() ,
,
設直線 ![]() 與平面
與平面 ![]() 所成角為
所成角為 ![]() ,則
,則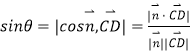
![]() ,
,
所以 ![]() 與平面
與平面 ![]() 所成角的正弦值為
所成角的正弦值為 ![]()
【解析】(Ⅰ)根據題目中所給的條件的特點,由△ABD和△CBD相似,可得∠ABD=∠CBD,AC⊥BD,即可得PO⊥AC,即PO⊥OB,又PO⊥BD.最后利用線面垂直的判定即可證得結論.
(Ⅱ)根據題意,以O為原點,建立空間直角坐標系O-xyz,求出平面PBC的法向量,利用向量夾角公式求解即可.


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:高中數學 來源: 題型:
【題目】我們可以用隨機模擬的方法估計π的值,如圖程序框圖表示其基本步驟(函數RAND是產生隨機數的函數,它能隨機產生(0,1)內的任何一個實數).若輸出的結果為521,則由此可估計π的近似值為( ) 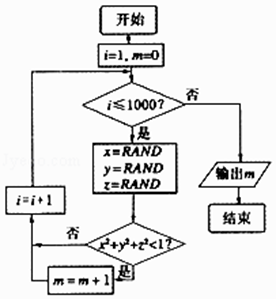
A.3.119
B.3.126
C.3.132
D.3.151
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,底面△ABC是等邊三角形,側面AA1B1B為正方形,且AA1⊥平面ABC,D為線段AB上的一點.
(Ⅰ) 若BC1∥平面A1CD,確定D的位置,并說明理由;
(Ⅱ) 在(Ⅰ)的條件下,求二面角A1D﹣C﹣BC1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知任意角
中,已知任意角![]() 以坐標原點
以坐標原點![]() 為頂點,
為頂點,![]() 軸的非負半軸為始邊,若終邊經過點
軸的非負半軸為始邊,若終邊經過點![]() ,且
,且![]() ,定義:
,定義:![]() ,稱“
,稱“![]() ”為“正余弦函數”,對于“正余弦函數
”為“正余弦函數”,對于“正余弦函數![]() ”,有同學得到以下性質:
”,有同學得到以下性質:
①該函數的值域為![]() ; ②該函數的圖象關于原點對稱;
; ②該函數的圖象關于原點對稱;
③該函數的圖象關于直線![]() 對稱; ④該函數為周期函數,且最小正周期為
對稱; ④該函數為周期函數,且最小正周期為![]() ;
;
⑤該函數的遞增區間為![]() .
.
其中正確的是__________.(填上所有正確性質的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+1|.
(Ⅰ) 解不等式f(x+8)≥10﹣f(x);
(Ⅱ) 若|x|>1,|y|<1,求證:f(y)<|x|f( ![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列{an}的前n項和為Sn , 且Sn滿足n(n+1)Sn2+(n2+n﹣1)Sn﹣1=0(n∈N*),則S1+S2+…+S2017= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com