【題目】已知函數f(x)的圖像與函數h(x)=
的圖像關于點Ａ（0，1）對稱。
（１）求函數f(x)的解析式；
（２）若g(x)＝xf(x)＋ax，且g(x)在區間（0,4］上為減函數，求實數a的取值范圍。
【答案】（1）
；（2）(－∞，－10].
【解析】試題分析：（1）利用函數關于點A（0，1）對稱，求出函數的解析式．
（2）利用二次函數的圖象和性質得到對稱軸與區間的關系．
試題解析：
(1)∵f(x)的圖象與h(x)的圖象關于點A(0,1)對稱，設f(x)圖象上任意一點坐標為B(x，y)，其關于A(0,1)的對稱點B′(x′，y′)，
則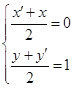
∴ 
∵B′(x′，y′)在h(x)上，∴y′＝x′＋
.
∴2－y＝－x－
，∴y＝x＋ +2，
即f(x) ＝x＋ +2.
(2)∵g(x)＝xf(x)+ax=x2+(a+2)x+1且g(x)在(0,4]上為減函數，
∴
≥4，
即a≤－10.
∴a的取值范圍為(－∞，－10]．
桃李文化快樂暑假武漢出版社系列答案
優秀生快樂假期每一天全新寒假作業本系列答案
暑假接力賽新疆青少年出版社系列答案科目：高中數學 來源： 題型：
【題目】近年來，空氣質量成為人們越來越關注的話題，空氣質量指數（
，簡稱
）是定量描述空氣質量狀況的指數，空氣質量按照
大小分為六級， 
為優； 
為良； 
為輕度污染； 
為中度污染； 
為重度污染；大于300為嚴重污染．環保部門記錄了2017年某月哈爾濱市10天的
的莖葉圖如下：
（1）利用該樣本估計該地本月空氣質量優良（
）的天數；（按這個月總共30天計算）
（2）現工作人員從這10天中空氣質量為優良的日子里隨機抽取2天進行某項研究，求抽取的2天中至少有一天空氣質量是優的概率；
（3）將頻率視為概率，從本月中隨機抽取3天，記空氣質量優良的天數為
，求
的概率分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
同時滿足：①對于定義域上的任意
，恒有
；②對于定義域上的任意
， 
，當
時，恒有
，則稱函數
為“理想函數”.在下列三個函數中：（1）
；（2）
；（3）
.“理想函數”有__________．（只填序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為
上的偶函數，當
時， 
.對于結論
（1）當
時， 
；（2）函數
的零點個數可以為4,5,7；
（3）若
，關于
的方程
有5個不同的實根，則
；
（4）若函數
在區間
上恒為正，則實數
的范圍是
.
說法正確的序號是__________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個正方體的平面展開圖及該正方體的直觀圖的示意圖如圖所示.在正方體中，設BC的中點為M，GH的中點為N.
(1)請將字母F，G，H標記在正方體相應的頂點處(不需說明理由).
(2)判斷平面BEG與平面ACH的位置關系，并證明你的結論.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，l是過定點P(4,2)且傾斜角為α的直線；在極坐標系(以坐標原點O為極點，
以x軸非負半軸為極軸，取相同單位長度)中，曲線C的極坐標方程為
.
(1)寫出直線l的參數方程，并將曲線C的方程化為直角坐標方程；
(2)若曲線C與直線相交于不同的兩點M，N，求|PM|＋|PN|的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為正整數，數列
滿足
，
，設數列
滿足
.
（1）求證：數列
為等比數列；
（2）若數列是等差數列，求實數
的值；
（3）若數列是等差數列，前項和為
，對任意的
，均存在
，使得
成立，求滿足條件的所有整數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】古希臘人常用小石子在沙灘上擺成各種形狀來研究數.比如：
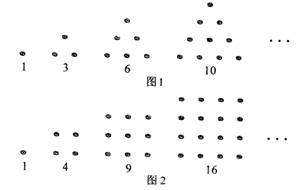
他們研究過圖1中的1，3，6，10，…，由于這些數能夠表示成三角形，將其稱為三角形數；類似的，稱圖2中的1，4，9，16，…這樣的數為正方形數.下列數中既是三角形數又是正方形數的是（ ）
A. 36 B. 45 C. 99 D. 100
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝x2＋
(x≠0，a∈R)．
(1)判斷函數f(x)的奇偶性；
(2)若f(x)在區間[2，＋∞)上是增函數，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com