
���}Ŀ����֪���タ![]() ����c(di��n)������(bi��o)ԭ�c(di��n)�����c(di��n)��
����c(di��n)������(bi��o)ԭ�c(di��n)�����c(di��n)��![]() �S�ϣ����^�c(di��n)
�S�ϣ����^�c(di��n)![]() .
.
��I����![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
������![]() ������(bi��o)ԭ�c(di��n)��
������(bi��o)ԭ�c(di��n)�� ![]() ��
��![]() �Ľ��c(di��n)���^�c(di��n)
�Ľ��c(di��n)���^�c(di��n)![]() �҃Aб�Ǟ�
�҃Aб�Ǟ�![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ��
�� ![]() ���c(di��n)����
���c(di��n)����![]() ����e.
����e.
���𰸡�(��) ![]() ��(��)
��(��) ![]() .
.
��������ԇ�}��������I�����c(di��n)����(bi��o)���뒁�タ������(sh��)p�����Ø�(bi��o)��(zh��n)���̣�������(j��)�c(di��n)бʽ��ֱ�����̣��c���タ(li��n)�����̽M�������f�_(d��)�����Լ����L(zh��ng)��ʽ���߅߅�L(zh��ng)������(j��)�c(di��n)��ֱ�����x��ʽ��ߣ���������������e��ʽ����e.
ԇ�}��������I�����}����O(sh��)���タ�ķ�����![]()
��?y��n)钁�タ![]() �^�c(di��n)
�^�c(di��n)![]() ������
������![]() �����
�����![]() ��
��
���Ԓ��タ![]() �ķ���
�ķ���![]()
����һ��
�ɣ�I���ã����c(di��n)![]() �����}��ֱ֪��
�����}��ֱ֪��![]() �ķ�����
�ķ�����![]() ��
��
(li��n)������![]() ����(ji��n)����
����(ji��n)����![]()
�O(sh��)![]() �t
�t![]() ��
��
�������L(zh��ng)��ʽ��![]() .
.
�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ��
��
����![]() ����e��
����e��![]() .
.
������
�ɣ�I���ã����c(di��n)![]() �����}��ֱ֪��
�����}��ֱ֪��![]() �ķ�����
�ķ�����![]() ��
��
(li��n)������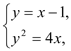 ����(ji��n)����
����(ji��n)����![]()
�O(sh��)![]() �t
�t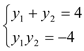 ��
��
���ø��a(b��)�����t![]() ����e��
����e��
![]()
������
�ɣ�I���ã����c(di��n)![]() �����}��ֱ֪��
�����}��ֱ֪��![]() �ķ�����
�ķ�����![]() ��
��
(li��n)������![]() ����(ji��n)����
����(ji��n)����![]()
�O(sh��)![]() ���f�_(d��)��������
���f�_(d��)��������![]() .
.
���Ò��タ���x����![]()
�c(di��n)![]() ��ֱ��
��ֱ��![]() �ľ��x
�ľ��x![]() ��
��
����![]() ����e��
����e��![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����푑�(y��ng)ʮ�Ŵ��(b��o)������Č�(sh��)ʩ�l(xi��ng)�����d��(zh��n)�ԣ�ij���fͶ�Y![]() �fԪ������һ���Gɫ�r(n��ng)�a(ch��n)Ʒ�ӹ��S.��(j��ng)�I(y��ng)�У���һ��֧��
�fԪ������һ���Gɫ�r(n��ng)�a(ch��n)Ʒ�ӹ��S.��(j��ng)�I(y��ng)�У���һ��֧��![]() �fԪ���Ժ�ÿ���֧������һ��������
�fԪ���Ժ�ÿ���֧������һ��������![]() �fԪ���ĵ�һ����ÿ���r(n��ng)��(ch��ng)Ʒ�N�������
�fԪ���ĵ�һ����ÿ���r(n��ng)��(ch��ng)Ʒ�N�������![]() �fԪ��ǰ
�fԪ��ǰ![]() ��ļ�����(r��n)�C��=ǰ
��ļ�����(r��n)�C��=ǰ![]() ��� ������-ǰ
��� ������-ǰ![]() ��Ŀ�֧��-Ͷ�Y�~
��Ŀ�֧��-Ͷ�Y�~![]() �fԪ��.
�fԪ��.
��1��ԓ�S�ĵڎ����_ʼӯ����
��2��ԓ�S�ڎ�����ƽ��������(r��n)�_(d��)����������ƽ��������(r��n)�����ֵ.
���𰸡�(1) �ĵ�![]() �_ʼӯ��(2) ԓ�S��
�_ʼӯ��(2) ԓ�S��![]() ����ƽ��������(r��n)�_(d��)�������ƽ��������(r��n)���ֵ��
����ƽ��������(r��n)�_(d��)�������ƽ��������(r��n)���ֵ��![]() �fԪ
�fԪ
��������ԇ�}������(1)����(j��)��ʽ�õ�![]() �����(sh��)ֵ����0��Å���(sh��)��������2������(j��)��ʽ�õ�
�����(sh��)ֵ����0��Å���(sh��)��������2������(j��)��ʽ�õ�![]() ���ɾ�ֵ����ʽ�õ�����(sh��)��ֵ.
���ɾ�ֵ����ʽ�õ�����(sh��)��ֵ.
������
���}���֪ǰ![]() ��ļ�����(r��n)����
��ļ�����(r��n)����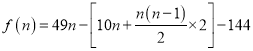
![]()
��1����![]() ����
����![]() �����
�����![]()
��![]() ֪���ĵ�
֪���ĵ�![]() �_ʼӯ��.
�_ʼӯ��.
��2����ƽ��������(r��n)![]()
��?y��n)?/span>![]() ����
����![]()
����![]()
��(d��ng)�҃H��(d��ng)![]() ����
����![]() �r(sh��)��̖(h��o)����.
�r(sh��)��̖(h��o)����.
��ƽ��������(r��n)���ֵ��![]() �fԪ��
�fԪ��
��ԓ�S��![]() ����ƽ��������(r��n)�_(d��)�������ƽ��������(r��n)���ֵ��
����ƽ��������(r��n)�_(d��)�������ƽ��������(r��n)���ֵ��![]() �fԪ.
�fԪ.
���}�͡�����}
���Y(ji��)����
21
���}Ŀ����֪��(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)�͞�
�(xi��ng)�͞�![]() �����ҝM��
�����ҝM��![]() ��
�� ![]() .
.
��1����(sh��)��![]() ͨ�(xi��ng)��ʽ��
ͨ�(xi��ng)��ʽ��
��2���O(sh��)![]() �锵(sh��)��
�锵(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)�ͣ����C��
�(xi��ng)�ͣ����C�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)f��x��=x3+ax2+bx+c�M��f'��0��=4��f'��-2��=0��
��1����a��b��ֵ������y=f��x�����c(di��n)��0��f��0����̎���о����̣�
��2��������(sh��)f��x��������(g��)��ͬ�����c(di��n)����c��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��ABC���J�������Σ����}p������ʽlogcosC ![]() ��0����������}q������ʽlogcosC
��0����������}q������ʽlogcosC ![]() ��0��������t��(f��)�����}p��q��p��q���Vp�У������}�Ă�(g��)��(sh��)�飨 ��
��0��������t��(f��)�����}p��q��p��q���Vp�У������}�Ă�(g��)��(sh��)�飨 ��
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�\(y��n)ݔ��˾��7�v���d![]() ��
��![]() �Ϳ�܇�c4�v���d
�Ϳ�܇�c4�v���d![]() ��
��![]() �Ϳ�܇����9���{�T������ij�θ��ٹ�·�У��˹�˾�а���ÿ�����ٰ��\(y��n)
�Ϳ�܇����9���{�T������ij�θ��ٹ�·�У��˹�˾�а���ÿ�����ٰ��\(y��n)![]() �r����΄�(w��)����֪ÿ�v��܇ÿ�������ĴΔ�(sh��)��
�r����΄�(w��)����֪ÿ�v��܇ÿ�������ĴΔ�(sh��)��![]() ��܇8����
��܇8���� ![]() ��܇6�Σ�ÿ�v��܇ÿ�������ijɱ��M(f��i)��
��܇6�Σ�ÿ�v��܇ÿ�������ijɱ��M(f��i)��![]() ��܇160Ԫ��
��܇160Ԫ�� ![]() ��܇252Ԫ��ÿ���ɳ�
��܇252Ԫ��ÿ���ɳ�![]() ��܇��
��܇��![]() ��܇�������v����˾�����ijɱ��M(f��i)�����
��܇�������v����˾�����ijɱ��M(f��i)�����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]()
��I����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
����������(sh��)![]() ��
��![]() �φ��{(di��o)�f����ԇ���
�φ��{(di��o)�f����ԇ���![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
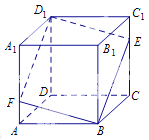
���}Ŀ����D��ʾ���������w![]() �У��c(di��n)
���c(di��n)![]() ����
����![]() �ϵ�һ��(g��)��(d��ng)�c(di��n)��ƽ��
�ϵ�һ��(g��)��(d��ng)�c(di��n)��ƽ��![]() ����
����![]() ���c(di��n)
���c(di��n)![]() ���o���������}��
���o���������}��
�ٴ����c(di��n)![]() ��ʹ��
��ʹ��![]() //ƽ��
//ƽ��![]() ��
��
����(du��)��������c(di��n)![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��
�������c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ��
��
�܌�(du��)��������c(di��n)![]() �������F
�������F![]() ���w�e����׃.
���w�e����׃.
�������_���}����̖(h��o)��______���������������_���}����̖(h��o)��.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����L(zh��ng)��2�ľ���AB�ăɂ�(g��)���c(di��n)�����c(di��n)��0�� ![]() ���齹�c(di��n)�Ē��タx2=2py���Ƅ�(d��ng)��ӛ����AB�����c(di��n)��M�����c(di��n)M��x�S����̾��x������˕r(sh��)�c(di��n)M������(bi��o)��
���齹�c(di��n)�Ē��タx2=2py���Ƅ�(d��ng)��ӛ����AB�����c(di��n)��M�����c(di��n)M��x�S����̾��x������˕r(sh��)�c(di��n)M������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����![]() �ǃɂ�(g��)�ཻƽ�棬�t���������}�У������}����̖(h��o)�� �����������������}����̖(h��o)��
�ǃɂ�(g��)�ཻƽ�棬�t���������}�У������}����̖(h��o)�� �����������������}����̖(h��o)��
����ֱ��![]() ���t��ƽ��
���t��ƽ��![]() ��(n��i)��һ���������cֱ��
��(n��i)��һ���������cֱ��![]() ƽ�е�ֱ����
ƽ�е�ֱ����
����ֱ��![]() ���t��ƽ��
���t��ƽ��![]() ��(n��i)��һ�����ڟo��(sh��)�lֱ���cֱ��
��(n��i)��һ�����ڟo��(sh��)�lֱ���cֱ��![]() ��ֱ��
��ֱ��
����ֱ��![]() ���t��ƽ��
���t��ƽ��![]() ��(n��i)����һ�������cֱ��
��(n��i)����һ�������cֱ��![]() ��ֱ��ֱ����
��ֱ��ֱ����
����ֱ��![]() ���t��ƽ��
���t��ƽ��![]() ��(n��i)��һ�������cֱ��
��(n��i)��һ�������cֱ��![]() ��ֱ��ֱ����
��ֱ��ֱ����
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com