
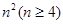 個正數排成
個正數排成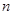 行
行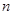 列:
列: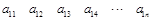
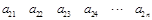
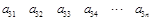
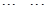
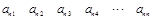
其中每一行的數由左至右成等差數列,每一列的數由上至下成等比數列,并且所有公比相等,已知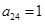 ,
,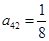 ,
,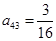 ,則
,則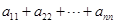 = 。
= 。
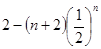
解析試題分析:設a11=a,第一行數的公差為d,第一列數的公比為q,可得ast=[a+(t-1)d]qs-1,又設第一行數列公差為d,各列數列的公比為q,則第四行數列公差是dq3,于是可得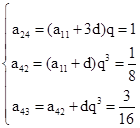 ,
,
解此方程組,得a11=d=q=±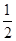 ,由于給n2個數都是正數,必有q>0,從而有a11=d=q=
,由于給n2個數都是正數,必有q>0,從而有a11=d=q=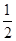 ,
,
于是對任意的1≤k≤n,有akk=a1kqk-1=[a11+(k-1)d]qk-1=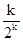 ,
,
得S=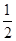 +
+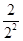 +……+
+……+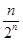 ,
,
又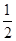 S=
S=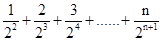 。
。
兩式相減后得: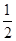 S=
S=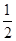 +
+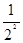 +……+
+……+ ,
,
所以S=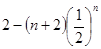 。
。
考點:本題主要考查等差數列、等比數列的基礎知識,“錯位相減法”。
點評:難題,通過觀察數列的特征,布列方程組,先求出數列的通項,從而根據數列通項的特點選擇合適的求和方法。“分組求和法”“裂項相消法”也常常考到的求和方法。


科目:高中數學 來源: 題型:填空題
下圖的數表滿足:①第n行首尾兩數均為n;②表中的遞推關系類似楊輝三角。則第n行 第2個數是_________.
第2個數是_________.
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5
6 16 25 25 16 6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com