在△ABC中,若sinA:sinB:sinC=5:7:8,則∠B的大小是 .
【答案】
分析:根據sinA:sinB:sinC=5:7:8,利用正弦定理可求得a,b,c的關系,進而設a=5k,b=7k,c=8k,代入余弦定理中求得cosB的值,進而求得B.
解答:解:sinA:sinB:sinC=5:7:8
∴a:b:c=5:7:8
設a=5k,b=7k,c=8k,
由余弦定理可得cosB=
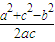
=

;
∴∠B=
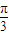
.
故答案為
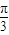
.
點評:本題主要考查了余弦定理和正弦定理的應用.作為解三角形中常用的公式,應熟練掌握正弦定理和余弦定理及其變形公式.
