以下四個命題:
①PA、PB是平面α的兩條長度相等的斜線段,則它們在平面α內的射影的長度必相等;
②平面α內的兩直線l1、l2,若l1、l2均與平面β平行,則α∥β;
③若平面α內有無數個點到平面β的距離相等,則α∥β;
④α、β為兩相交平面,且α不垂直于β,α內有一定直線l,則在平面β內有無數條直線與l垂直.
其中正確的命題的個數是( )
A.1個
B.2個
C.3個
D.4個
【答案】
分析:根據空間平行與垂直的有關定理,對各個選項逐個加以判斷:利用線面垂直的定義,通過計算可得①正確;根據面面平行的判定定理,可得②錯;根據平行于平面的直線到平面距離相等,可以舉出反例說明③錯;根據異面直線所成角的含義,可以結合已知條件作出輔助線,從而證出④正確.
解答:解:對于①,設點P到平面α的距離等于d,可得
斜線段PA在平面α內的射影長為:
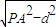
,
同理可得PB在平面α內的射影長:
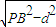
,
若PA=PB,則PA、PB平面α內的射影的長度必相等,故①正確;
對于②,若平面α內的相交直線l
1、l
2,且l
1、l
2均與平面β平行,則α∥β
但沒有相交這個條件,換成l
1∥l
2結論就不一定成立,故②錯;
對于③,若平面α與平面β垂直相交,在平面α內作出交線的平行線m,
則直線m上有無數個點到平面β的距離相等,說明平面α內有無數個點到平面β的距離相等,
但結論“α∥β”不成立,故③錯;
對于④,α、β為兩相交平面,設它們的交線是m,在平面β內可作出m的垂線n,
并且這樣的垂線有無數條,那只要直線l在α內與m保持平行,則必有l⊥n,
即便是α不垂直于β,在α內有也存在直線l,與平面β內無數條直線垂直,故④正確.
綜上,得正確的選項是①④
故選B
點評:本題以命題真假的判斷為載體,考查了立體幾何中空間的平行與垂直位置關系的判斷,屬于基礎題.考查了推理證明的能力和空間想象能力.

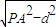 ,
,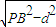 ,
,
