
 <θ<
<θ<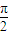 )在復平面上對應向量
)在復平面上對應向量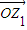 ,將
,將 按順時針方向旋轉
按順時針方向旋轉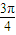 后得到向量
后得到向量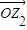 ,
,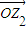 對應的復數為z2=r(cosφ+isinφ),則tanφ= .
對應的復數為z2=r(cosφ+isinφ),則tanφ= .  π+β ),sin∅=sin(
π+β ),sin∅=sin(  π+β),可求tan∅,再把tanβ=
π+β),可求tan∅,再把tanβ=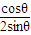 代入化簡.
代入化簡.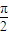 ) 的模為
) 的模為  =
=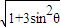 ,
, (
( 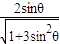 +i
+i 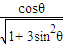 )=
)=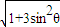 (cosβ+i sinβ)
(cosβ+i sinβ) ,sinβ=
,sinβ=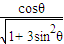 ,β為銳角,∴tanβ=
,β為銳角,∴tanβ=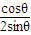 ,
, •(cos(β-
•(cos(β-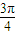 )+i sin(β-
)+i sin(β-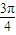 ))
)) 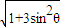 •(cos(2π+β-
•(cos(2π+β-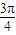 )+i sin(2π+β-
)+i sin(2π+β-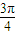 ))=
))= •(cos(
•(cos(  π+β )+isin(
π+β )+isin(  π+β)),
π+β)), π+β ),sin∅=sin(
π+β ),sin∅=sin(  π+β),
π+β),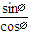 =
=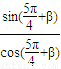 =tan(
=tan(  +β)=tan(
+β)=tan(  +β)=
+β)= =
=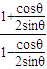 =
=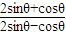
 ,
,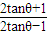 .
.

 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:高中數學 來源: 題型:
| π |
| 4 |
| π |
| 2 |
| OZ1 |
| OZ1 |
| 3π |
| 4 |
| OZ2 |
| OZ2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 2 |
| oz1 |
| oz1 |
| 3 |
| 4 |
| oz2 |
| oz2 |
| A、+12tgθ-1 | ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中數學 來源: 題型:013
設復數z1=2sinθ+icosθ(![]() <θ<
<θ<![]()
![]() 在復平面上對應向量
在復平面上對應向量![]() ,將
,將![]() 按順時針方向旋轉
按順時針方向旋轉![]() π后得到向量
π后得到向量![]() ,
,![]() 對應的復數為z2=
對應的復數為z2=
r(cos![]() +isin
+isin![]() ),則tan
),則tan![]() 等于(
)
等于(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:013
r(cos![]() +isin
+isin![]() ),則tan
),則tan![]() 等于(
)
等于(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com