
【題目】設函數f(x)=(x﹣a)(x﹣b)(x﹣c)(其中a>1,b>1),x=0是f(x)的一個零點,曲線y=f(x)在點(1,f(1))處的切線平行于x軸,則a+b的最小值為 .
科目:高中數學 來源: 題型:
【題目】設關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是從0,1,2,3,4五個數中任取的一個數,
是從0,1,2,3,4五個數中任取的一個數,![]() 是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
(2)若![]() 是從區間
是從區間![]() 上任取的一個數,
上任取的一個數,![]() 是從區間
是從區間![]() 上任取的一個數,求上述方程有實根的概率.
上任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個結論: ① ![]() (x2+sinx)dx=18,則a=3;
(x2+sinx)dx=18,則a=3;
②用相關指數R2來刻畫回歸效果,R2的值越大,說明模型的擬合效果越差;
③若f(x)是定義在R上的奇函數,且滿足f(x+2)=﹣f(x),則函數f(x)的圖象關于x=1對稱;
④已知隨機變量ξ服從正態分布N(1,σ2),P(ξ≤4)=0.79,則P(ξ<﹣2)=0.21;
其中正確結論的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖為中國傳統智力玩具魯班鎖,起源于古代漢族建筑中首創的榫卯結構,這種三維的拼插器具內部的凹凸部分(即榫卯結構)嚙合,外觀看是嚴絲合縫的十字立方體,其上下、左右、前后完全對稱,六根完全相同的正四棱柱分成三組,經90°榫卯起來.現有一魯班鎖的正四棱柱的底面正方形邊長為1,欲將其放入球形容器內(容器壁的厚度忽略不計),若球形容器表面積的最小值為30π,則正四棱柱體的高為( ) 
A.![]()
B.![]()
C.![]()
D.5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣3)ex+ax,a∈R. (Ⅰ)當a=1時,求曲線f(x)在點(2,f(2))處的切線方程;
(Ⅱ)當a∈[0,e)時,設函數f(x)在(1,+∞)上的最小值為g(a),求函數g(a)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)=x+ ![]() (x>0)都在x=x0處取得最小值.
(x>0)都在x=x0處取得最小值.
(1)求f(x0)﹣g(x0)的值.
(2)設函數h(x)=f(x)﹣g(x),h(x)的極值點之和落在區間(k,k+1),k∈N,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為評估兩套促銷活動方案(方案1運作費用為5元/件;方案2的運作費用為2元/件),在某地區部分營銷網點進行試點(每個試點網點只采用一種促銷活動方案),運作一年后,對比該地區上一年度的銷售情況,制作相應的等高條形圖如圖所示. 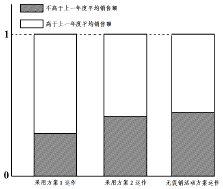
(1)請根據等高條形圖提供的信息,為該公司今年選擇一套較為有利的促銷活動方案(不必說明理由);
(2)已知該公司產品的成本為10元/件(未包括促銷活動運作費用),為制定本年度該地區的產品銷售價格,統計上一年度的8組售價xi(單位:元/件,整數)和銷量yi(單位:件)(i=1,2,…,8)如下表所示:
售價x | 33 | 35 | 37 | 39 | 41 | 43 | 45 | 47 |
銷量y | 840 | 800 | 740 | 695 | 640 | 580 | 525 | 460 |
①請根據下列數據計算相應的相關指數R2 , 并根據計算結果,選擇合適的回歸模型進行擬合;
②根據所選回歸模型,分析售價x定為多少時?利潤z可以達到最大.
| | | |
| 49428.74 | 11512.43 | 175.26 |
| 124650 | ||
(附:相關指數  )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是首項為1,公差為2的等差數列,{bn}是首項為1,公比為q的等比數列.記cn=an+bn , n=1,2,3,….
(1)若{cn}是等差數列,求q的值;
(2)求數列{cn}的前n項和Sn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com