
【題目】已知圓![]() :
: ![]() 過橢圓
過橢圓![]() :
: ![]() (
(![]() )的短軸端點,
)的短軸端點, ![]() ,
, ![]() 分別是圓
分別是圓![]() 與橢圓
與橢圓![]() 上任意兩點,且線段
上任意兩點,且線段![]() 長度的最大值為3.
長度的最大值為3.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 作圓
作圓![]() 的一條切線交橢圓
的一條切線交橢圓![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 的面積的最大值.
的面積的最大值.
【答案】(Ⅰ)![]() (Ⅱ)1.
(Ⅱ)1.
【解析】試題分析: (Ⅰ)根據橢圓幾何性質得線段![]() 長度的最大值為
長度的最大值為![]() ,且
,且![]() ,解出
,解出![]() ,得橢圓
,得橢圓![]() 的方程;(Ⅱ)利用點斜式設直線方程,與橢圓方程聯立,結合韋達定理及弦長公式可得底邊
的方程;(Ⅱ)利用點斜式設直線方程,與橢圓方程聯立,結合韋達定理及弦長公式可得底邊![]() 長(用斜率及
長(用斜率及![]() 表示);利用點到直線距離公式得三角形的高(用斜率及
表示);利用點到直線距離公式得三角形的高(用斜率及![]() 表示);根據圓心到切線距離等于半徑得斜率與
表示);根據圓心到切線距離等于半徑得斜率與![]() 關系,代入面積公式并化簡得關于
關系,代入面積公式并化簡得關于![]() 的函數關系式,最后利用基本不等式求最值.
的函數關系式,最后利用基本不等式求最值.
試題解析:解:(Ⅰ)∵圓![]() 過橢圓
過橢圓![]() 的短軸端點,∴
的短軸端點,∴![]() ,又∵線段
,又∵線段![]() 長度的最大值為3,
長度的最大值為3,
∴![]() ,即
,即![]() ,
,
∴橢圓![]() 的標準方程為
的標準方程為![]() .
.
(Ⅱ)由題意可設切線![]() 的方程為
的方程為![]() ,即
,即![]() ,則
,則![]() ,得
,得![]() .①
.①
聯立得方程組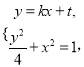 消去
消去![]() 整理得
整理得![]() .
.
其中![]() ,
,
設![]() ,
, ![]() ,則
,則![]() ,
, ![]() ,
,
則![]() .②
.②
將①代入②得![]() ,∴
,∴![]() ,
,
而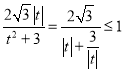 ,等號成立當且僅當
,等號成立當且僅當![]() ,即
,即![]() .
.
綜上可知: ![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切線在x軸、y軸上截距相等,求切線的方程.
(2)從圓外一點P(x0,y0)向圓引切線PM,M為切點,O為原點,若|PM|=|PO|,求使|PM|最小的P點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:f(x)=2/(x-m)在區間(1,+∞)上是減函數;;命題q:2x-1+2m>0對任意x∈R恒成立.若(![]() p)∧q為真,求實數m的取值范圍。
p)∧q為真,求實數m的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (m,n∈R)在x=1處取得極值2.
(m,n∈R)在x=1處取得極值2.
(1)求f(x)的解析式;
(2)k為何值時,方程f(x)-k=0只有1個根
(3)設函數g(x)=x2-2ax+a,若對于任意x1∈R,總存在x2∈[-1,0],使得g(x2)≤f(x1),求a的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
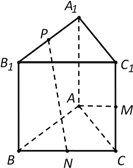
【題目】如圖,直三棱柱ABC-A1B1C1中, AB=AC=AA1,AB⊥AC,M是CC1的中點,N是BC的中點,點P在線段A1B1上運動.
(Ⅰ)求證:PN⊥AM;
(Ⅱ)試確定點P的位置,使直線PN和平面ABC所成的角
最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() 為常數,
為常數,![]() ).(Ⅰ)求函數
).(Ⅰ)求函數![]() 的單調區間;(Ⅱ)當
的單調區間;(Ⅱ)當![]() 時,是否存在實數
時,是否存在實數![]() ,使得當
,使得當![]() 時,不等式
時,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范圍;如果不存在,請說明理由(其中
的取值范圍;如果不存在,請說明理由(其中![]() 是自然對數的底數,
是自然對數的底數,![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子元件廠對一批新產品的使用壽命進行檢驗,并且廠家規定使用壽命在![]() 為合格品,使用壽命超過500小時為優質品,質檢科抽取了一部分產品做樣本,經檢測統計后,繪制出了該產品使用壽命的頻率分布直方圖(如圖):
為合格品,使用壽命超過500小時為優質品,質檢科抽取了一部分產品做樣本,經檢測統計后,繪制出了該產品使用壽命的頻率分布直方圖(如圖):
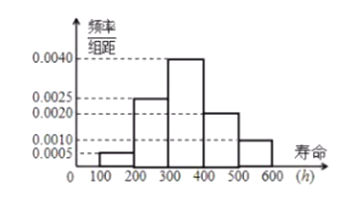
(1)根據頻率分布直方圖估計該廠產品為合格品或優質品的概率,并估計該批產品的平均使用壽命;
(2)從這批產品中,采取隨機抽樣的方法每次抽取一件產品,抽取4次,若以上述頻率作為概率,記隨機變量![]() 為抽出的優質品的個數,列出
為抽出的優質品的個數,列出![]() 的分布列,并求出其數學期望.
的分布列,并求出其數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com