【題目】已知橢圓
過點
，且離心率為
.直線
與
軸正半軸和
軸分別交于點
、
，與橢圓分別交于點
、
，各點均不重合且滿足
，
.
（1）求橢圓的標準方程；
（2）若
，試證明:直線過定點并求此定點.
新思維假期作業暑假吉林大學出版社系列答案
藍天教育暑假優化學習系列答案科目：高中數學 來源： 題型：
【題目】為提高產品質量，某企業質量管理部門經常不定期地對產品進行抽查檢測，現對某條生產線上隨機抽取的100個產品進行相關數據的對比，并對每個產品進行綜合評分（滿分100分），將每個產品所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為80分及以上的產品為一等品.
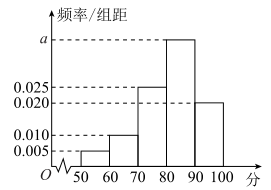
（1）求圖中
的值，并求綜合評分的中位數；
（2）用樣本估計總體，視頻率作為概率，在該條生產線中隨機抽取3個產品，求所抽取的產品中一等品數的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
的右焦點到漸近線的距離為3.現有如下條件：①雙曲線
的離心率為
； ②雙曲線與橢圓
共焦點； ③雙曲線右支上的一點
到
的距離之差是虛軸長的
倍.
請從上述3個條件中任選一個，得到雙曲線的方程為_____________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，射線
與圓
交于點
，橢圓
的方程為
，以極點為原點，極軸為
軸正半軸建立平面直角坐標系
（1）求點的直角坐標和橢圓的參數方程；
（2）若
為橢圓的下頂點，
為橢圓上任意一點，求
的取值范圍
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝alnx－bx2，a，b∈R.若不等式f(x)≥x對所有的b∈(－∞，0]，x∈(e，e2]都成立，則實數a的取值范圍是( )
A. [e，＋∞)B. [
，＋∞)
C. [，e2)D. [e2，＋∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
