
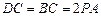 ,
,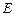 為DB的中點,
為DB的中點,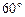 ,若存在,試確定點F的位置,若不存在,說明理由.
,若存在,試確定點F的位置,若不存在,說明理由.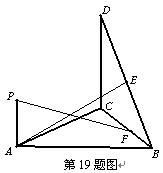
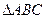 為等邊三角形,所以BC⊥AO ……………………………………………3分
為等邊三角形,所以BC⊥AO ……………………………………………3分
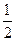 DC
DC PA,故四邊形APEO為矩形 …………………………………………7分
PA,故四邊形APEO為矩形 …………………………………………7分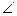 PFE為PF與面DBC所成的角,即
PFE為PF與面DBC所成的角,即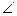 PFE=
PFE=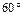 …9分
…9分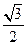 BC,故EF=
BC,故EF=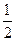 BC,
BC,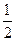 DC,又E為BD的中點,
DC,又E為BD的中點,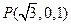 ,設
,設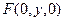 ,
,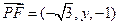 ,………………………………………………………………………7分
,………………………………………………………………………7分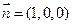 ,則由
,則由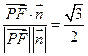 ,………………………………………………………………………..9分
,………………………………………………………………………..9分

科目:高中數學 來源:不詳 題型:解答題
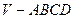 中,底面
中,底面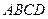 是邊長為2的正方形,其余四個側面都是側棱長為
是邊長為2的正方形,其余四個側面都是側棱長為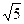 的等腰三角形,且
的等腰三角形,且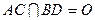 .
.
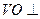 平面
平面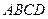 ;
;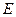 是
是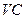 的中點,求
的中點,求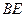 與平面
與平面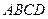 所成角的正切值.
所成角的正切值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
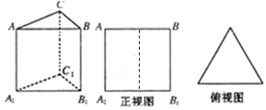
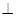 底面A1B1C1,主視圖是邊長為2的正方形,該三棱柱的左視圖面積為
底面A1B1C1,主視圖是邊長為2的正方形,該三棱柱的左視圖面積為 A.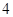 | B.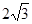 |
C.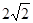 | D.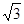 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
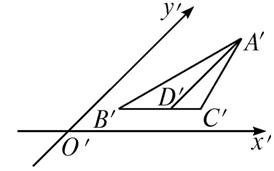
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com