
【題目】已知離心率為![]() 的橢圓
的橢圓![]() 的左頂點為
的左頂點為![]() ,且橢圓
,且橢圓![]() 經(jīng)過點
經(jīng)過點![]() ,與坐標(biāo)軸不垂直的直線
,與坐標(biāo)軸不垂直的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點.
兩點.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)若直線![]() 和直線
和直線![]() 的斜率之積為
的斜率之積為![]() ,求證:直線
,求證:直線![]() 過定點;
過定點;
(3)若![]() 為橢圓
為橢圓![]() 上一點,且
上一點,且![]() ,求三角形
,求三角形![]() 的面積.
的面積.
【答案】(1)![]() ;(2)證明見解析;(3)
;(2)證明見解析;(3)![]() .
.
【解析】
(1)根據(jù)離心率,將![]() 用
用![]() 表示,橢圓方程化為
表示,橢圓方程化為![]() ,點
,點![]() 代入方程,即可求出橢圓
代入方程,即可求出橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)![]() 的方程為
的方程為![]() ,(或
,(或![]() ),設(shè)
),設(shè)![]() ,將直線方程與橢圓方程聯(lián)立,消元得到
,將直線方程與橢圓方程聯(lián)立,消元得到![]() ,由
,由![]() ,得
,得![]() ,且
,且![]() ,
,![]() ,
,![]() ,整理得
,整理得![]() ,
,![]() 或
或![]() (舍),滿足
(舍),滿足![]() ,可得直線過定點
,可得直線過定點![]()
(3)![]() ,根據(jù)向量的關(guān)系可得
,根據(jù)向量的關(guān)系可得![]() ,點
,點![]() 到直線
到直線![]() 距離
距離![]() ,
,![]() 即可求解;或?qū)⒏鶕?jù)橢圓的參數(shù)方程,設(shè)
即可求解;或?qū)⒏鶕?jù)橢圓的參數(shù)方程,設(shè)![]() ,
,![]() ,
,![]() ,求得點
,求得點![]() ,又點
,又點![]() 在橢圓上,整理可得
在橢圓上,整理可得![]() ,將
,將![]() 用
用![]() 表示,并化簡為
表示,并化簡為![]() ,即可求得結(jié)論.
,即可求得結(jié)論.
(1)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,又∵橢圓
,又∵橢圓![]() 經(jīng)過點
經(jīng)過點![]() ,
,
∴![]() ,∴橢圓
,∴橢圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() ;
;
(2)方法一:![]() 的方程為
的方程為![]() ,設(shè)
,設(shè)![]() ,
,
聯(lián)立方程組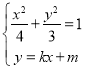 ,化簡得
,化簡得![]() ,
,
由![]() 解得
解得![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
化簡可得:![]() ,∴
,∴![]() 或
或![]() (舍),滿足
(舍),滿足![]() ,
,
∴直線![]() 的方程為
的方程為![]() ,
,
∴直線![]() 經(jīng)過定點
經(jīng)過定點![]() .
.
方法二:設(shè)![]() 的方程為
的方程為![]() ,設(shè)
,設(shè)![]() ,
,
聯(lián)立方程組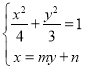 ,化簡得
,化簡得![]() ,
,
![]() 解得:
解得:![]() ,且
,且![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
化簡可得:![]() ,∴
,∴![]() 或者
或者![]() (舍)滿足
(舍)滿足![]()
∴直線![]() 經(jīng)過定點
經(jīng)過定點![]() ;
;
方法三:設(shè)![]() ,則有
,則有![]() ,∴
,∴![]() ,
,
設(shè)![]() 方程為
方程為![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴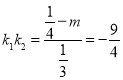 ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴直線![]() 經(jīng)過定點
經(jīng)過定點![]() ;
;
(3)點![]() 到直線
到直線![]() 距離
距離![]() ,
,
∴![]() ,∴
,∴![]() ;
;
方法二:設(shè)![]() ,
,
∵![]() ,∴點
,∴點![]() ,
,
又∵點![]() 在橢圓
在橢圓![]() 上,∴
上,∴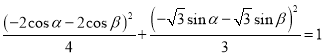 ,
,
∴![]() .
.
![]()
![]() ,
,
∴![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)等差數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,在同一個坐標(biāo)系中,
,在同一個坐標(biāo)系中,![]() 及
及![]() 的部分圖象如圖所示,則( ).
的部分圖象如圖所示,則( ).

A. 當(dāng)![]() 時,
時,![]() 取得最大值 B. 當(dāng)
取得最大值 B. 當(dāng)![]() 時,
時,![]() 取得最大值
取得最大值
C. 當(dāng)![]() 時,
時,![]() 取得最小值 D. 當(dāng)
取得最小值 D. 當(dāng)![]() 時,
時,![]() 取得最小值
取得最小值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)全集![]() ,關(guān)于
,關(guān)于![]() 的不等式
的不等式![]() (
(![]() )的解集為
)的解集為![]() .
.
(1)求集合![]() ;
;
(2)設(shè)集合![]() ,若
,若![]() 中有且只有三個元素,求實數(shù)
中有且只有三個元素,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國有十二生肖,又叫十二屬相,每一個人的出生年份對應(yīng)了十二種動物(鼠、牛、虎、兔、龍、蛇、馬、羊、猴、雞、狗、豬)的一種,現(xiàn)有十二生肖的吉物各一個,甲、乙、丙三位同學(xué)依次選一個作為禮物,甲同學(xué)喜歡牛和馬,乙同學(xué)喜歡牛、兔、狗和羊,丙同學(xué)哪個吉祥物都喜歡,如果讓三位同學(xué)選取的禮物都滿意,那么不同的選法有( )
A. 50種B. 60種C. 70種D. 90種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在發(fā)生某公共衛(wèi)生事件期間,有專業(yè)機構(gòu)認(rèn)為該事件在一段時間內(nèi)沒有發(fā)生大規(guī)模群體感染的標(biāo)志是“連續(xù)10日,每天新增疑似病例不超過7人”.過去10日,甲、乙、丙、丁四地新增疑似病例數(shù)據(jù)信息如下:
甲地:總體平均數(shù)為3,中位數(shù)為4;
乙地:總體平均數(shù)為1,總體方差大于0;
丙地:總體平均數(shù)為2,總體方差為3;
丁地:中位數(shù)為2,眾數(shù)為3;
則甲、乙、兩、丁四地中,一定沒有發(fā)生大規(guī)模群體感染的是( )
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 為自然對數(shù)的底數(shù)),
為自然對數(shù)的底數(shù)),![]() .
.
(Ⅰ)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間和極值;
的單調(diào)區(qū)間和極值;
(Ⅱ)已知函數(shù)![]() 在
在![]() 上為增函數(shù),且
上為增函數(shù),且![]() ,若在
,若在![]() 上至少存在一個實數(shù)
上至少存在一個實數(shù)![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】數(shù)列{an}滿足:a1=![]() ,a2=
,a2=![]() ,且a1a2+a2a3+…+anan+1=na1an+1對任何的正整數(shù)n都成立,則
,且a1a2+a2a3+…+anan+1=na1an+1對任何的正整數(shù)n都成立,則![]() 的值為( )
的值為( )
A. 5032 B. 5044 C. 5048 D. 5050
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以該直角坐標(biāo)系的原點
為參數(shù)),以該直角坐標(biāo)系的原點![]() 為極點,
為極點,![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,射線![]() 的普通方程為
的普通方程為![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以O為極點,x軸的正半軸為極軸建立極坐標(biāo)系,曲線
為參數(shù)).以O為極點,x軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出![]() 與
與![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)設(shè)![]() 與
與![]() 的交點為P(點P不為極點),
的交點為P(點P不為極點),![]() 與
與![]() 的交點為Q,當(dāng)
的交點為Q,當(dāng)![]() 在
在![]() 上變化時,求
上變化時,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com