
【題目】2019年第十三屆女排世界杯共12支參賽球隊,比賽賽制釆取單循環方式,即每支球隊進行11場比賽,最后靠積分選出最后冠軍.積分規則如下(比賽采取5局3勝制):比賽中以3—0或3—1取勝的球隊積3分,負隊積0分;而在比賽中以3—2取勝的球隊積2分,負隊積1分.9輪過后,積分榜上的前2名分別為中國隊和美國隊,中國隊積26分,美國隊積22分.第10輪中國隊對抗塞爾維亞隊,設每局比賽中國隊取勝的概率為![]() .
.
(1)第10輪比賽中,記中國隊3—1取勝的概率為![]() ,求
,求![]() 的最大值點
的最大值點![]() .
.
(2)以(1)中的![]() 作為
作為![]() 的值.
的值.
(i)在第10輪比賽中,中國隊所得積分為![]() ,求
,求![]() 的分布列;
的分布列;
(ⅱ)已知第10輪美國隊積3分,判斷中國隊能否提前一輪奪得冠軍(第10輪過后,無論最后一輪即第11輪結果如何,中國隊積分最多)?若能,求出相應的概率;若不能,請說明理由.
【答案】(1)見解析(2)(i)見解析(ⅱ)見解析
【解析】
(1)先得出![]() ,結合導數得出函數
,結合導數得出函數![]() 的單調性,進而得出
的單調性,進而得出![]() 的最大值點
的最大值點![]() ;
;
(2)(i)先得出![]() 的可能取值,再得出其相應概率,列出分布列即可;
的可能取值,再得出其相應概率,列出分布列即可;
(ⅱ)若中國隊在第10輪比賽中,獲得![]() 積分,則總積分為
積分,則總積分為![]() 分,即便美國隊第
分,即便美國隊第![]() 都獲得
都獲得![]() 分,則總積分為
分,則總積分為![]() 分,則中國隊可以提前一輪奪得冠軍,最后由(i)得出其概率.
分,則中國隊可以提前一輪奪得冠軍,最后由(i)得出其概率.
(1)![]()
由此![]()
令![]() ,得
,得![]()
當![]() 時,
時,![]() 在
在![]() 上為增函數;
上為增函數;
當![]() 時,
時,![]() 在
在![]() 上為減函數;
上為減函數;
所以![]() 的最大值點
的最大值點![]()
(2)由(1)知![]()
(i)![]() 可取
可取![]()
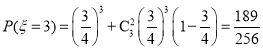
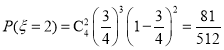
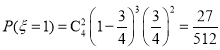
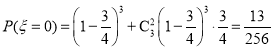
所以![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
(ⅱ)若![]() ,則中國隊
,則中國隊![]() 輪后的總積分為
輪后的總積分為![]() 分,美國隊即便第
分,美國隊即便第![]() 輪和第
輪和第![]() 輪都積
輪都積![]() 分,則
分,則![]() 輪過后的總積分是
輪過后的總積分是![]() 分,
分,![]() ,所以,中國隊如果第
,所以,中國隊如果第![]() 輪積
輪積![]() 分,則可提前一輪奪得冠軍,其概率為
分,則可提前一輪奪得冠軍,其概率為![]()


科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是R上的奇函數且單調遞增,則下列函數是偶函數且在(0,+∞)上單調遞增的有( )
①y=|f(x)|;
②y=f(x2+x);
③y=f(|x|);
④y=ef(x)+e﹣f(x).
A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了提高生產線的運行效率,工廠對生產線的設備進行了技術改造.為了對比技術改造后的效果,采集了生產線的技術改造前后各20次連續正常運行的時間長度(單位:天)數據,并繪制了如下莖葉圖:
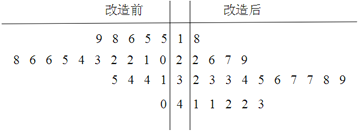
(Ⅰ)(1)設所采集的40個連續正常運行時間的中位數![]() ,并將連續正常運行時間超過
,并將連續正常運行時間超過![]() 和不超過
和不超過![]() 的次數填入下面的列聯表:
的次數填入下面的列聯表:
超過 | 不超過 | |
改造前 |
|
|
改造后 |
|
|
試寫出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根據(1)中的列聯表,能否有![]() 的把握認為生產線技術改造前后的連續正常運行時間有差異?
的把握認為生產線技術改造前后的連續正常運行時間有差異?
附: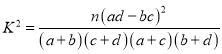 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工廠的生產線的運行需要進行維護.工廠對生產線的生產維護費用包括正常維護費、保障維護費兩種對生產線設定維護周期為![]() 天(即從開工運行到第
天(即從開工運行到第![]() 天(
天(![]() )進行維護.生產線在一個生產周期內設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內,若生產線能連續運行,則不會產生保障維護費;若生產線不能連續運行,則產生保障維護費.經測算,正常維護費為0.5萬元
)進行維護.生產線在一個生產周期內設置幾個維護周期,每個維護周期相互獨立.在一個維護周期內,若生產線能連續運行,則不會產生保障維護費;若生產線不能連續運行,則產生保障維護費.經測算,正常維護費為0.5萬元![]() 次;保障維護費第一次為0.2萬元
次;保障維護費第一次為0.2萬元![]() 周期,此后每增加一次則保障維護費增加0.2萬元.現制定生產線一個生產周期(以120天計)內的維護方案:
周期,此后每增加一次則保障維護費增加0.2萬元.現制定生產線一個生產周期(以120天計)內的維護方案:![]() ,
,![]() ,2,3,4.以生產線在技術改造后一個維護周期內能連續正常運行的頻率作為概率,求一個生產周期內生產維護費的分布列及期望值.
,2,3,4.以生產線在技術改造后一個維護周期內能連續正常運行的頻率作為概率,求一個生產周期內生產維護費的分布列及期望值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com