
【題目】在四棱錐![]() 中,
中,![]() 與
與![]() 相交于點
相交于點![]() ,點
,點![]() 在線段
在線段![]() 上,
上,![]() .
.
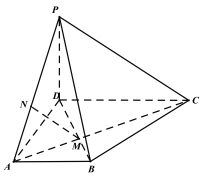
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)詳見解析;(2)![]() .
.
【解析】
(1)根據平行線等分線段可得![]() ,再根據線面平行的判定定理即可證明;
,再根據線面平行的判定定理即可證明;
(2)由題意可得![]() 為等邊三角形,則
為等邊三角形,則![]() 由勾股定理可得
由勾股定理可得![]() 且
且![]() ,則
,則![]() ,
,
(方法一)從而平面![]() 平面
平面![]() ,作
,作![]() 于
于![]() ,可證得
,可證得![]() 即為
即為![]() 到平面
到平面![]() 的距離,由此可求出答案.
的距離,由此可求出答案.
(方法二)設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,由三棱錐的體積公式可得
,由三棱錐的體積公式可得![]() ,即
,即![]() ,代入數據即可求出答案.
,代入數據即可求出答案.
(1)證:![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ;
;
(2)解:(方法一)∵![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() 且
且![]() ,
,
又∵![]() ,
,
∴![]()
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
作![]() 于
于![]() ,
,
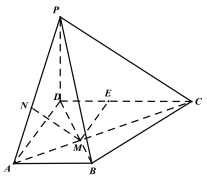
∵平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 即為
即為![]() 到平面
到平面![]() 的距離,
的距離,
在![]() 中,設
中,設![]() 邊上的高為
邊上的高為![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.
(方法二)∵![]() ,
,
∴![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() 且
且![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() .
.
設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,由
,由![]() 得
得![]() ,
,
∴![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.


科目:高中數學 來源: 題型:
【題目】在全面建成小康社會的決勝階段,讓貧困地區同全國人民共同進入全面小康社會是我們黨的莊嚴承諾.在“脫真貧、真脫貧”的過程中,精準扶貧助推社會公平顯得尤其重要.若某農村地區有200戶貧困戶,經過一年扶貧后,對該地區的“精準扶貧”的成效檢查驗收.從這200戶貧困戶中隨機抽出50戶,對各戶的人均年收入(單位:千元)進行調查得到如下頻數表:
人均年收入 |
|
|
|
|
|
|
頻數 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定為貧困戶,人均年收入在4000元~8000元的判定為脫貧戶,人均年收入達到8000元的判定為小康戶.
(1)用樣本估計總體,估計該地區還有多少戶沒有脫貧;
(2)為了了解未脫貧的原因,從抽取的50戶中用分層抽樣的方法抽10戶進行調研.
①貧困戶、脫貧戶、小康戶分別抽到的人數是多少?
②從被抽到的脫貧戶和小康戶中各選1人做經驗介紹,求小康戶中人均年收入最高的一戶被選到的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年第十三屆女排世界杯共12支參賽球隊,比賽賽制釆取單循環方式,即每支球隊進行11場比賽,最后靠積分選出最后冠軍.積分規則如下(比賽采取5局3勝制):比賽中以3—0或3—1取勝的球隊積3分,負隊積0分;而在比賽中以3—2取勝的球隊積2分,負隊積1分.9輪過后,積分榜上的前2名分別為中國隊和美國隊,中國隊積26分,美國隊積22分.第10輪中國隊對抗塞爾維亞隊,設每局比賽中國隊取勝的概率為![]() .
.
(1)第10輪比賽中,記中國隊3—1取勝的概率為![]() ,求
,求![]() 的最大值點
的最大值點![]() .
.
(2)以(1)中的![]() 作為
作為![]() 的值.
的值.
(i)在第10輪比賽中,中國隊所得積分為![]() ,求
,求![]() 的分布列;
的分布列;
(ⅱ)已知第10輪美國隊積3分,判斷中國隊能否提前一輪奪得冠軍(第10輪過后,無論最后一輪即第11輪結果如何,中國隊積分最多)?若能,求出相應的概率;若不能,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】體溫是人體健康狀況的直接反應,一般認為成年人腋下溫度T(單位:![]() )平均在
)平均在![]() 之間即為正常體溫,超過
之間即為正常體溫,超過![]() 即為發熱.發熱狀態下,不同體溫可分成以下三種發熱類型:低熱:
即為發熱.發熱狀態下,不同體溫可分成以下三種發熱類型:低熱:![]() ;高熱:
;高熱:![]() ;超高熱(有生命危險):
;超高熱(有生命危險):![]() .某位患者因患肺炎發熱,于12日至26日住院治療.醫生根據病情變化,從14日開始,以3天為一個療程,分別用三種不同的抗生素為該患者進行消炎退熱.住院期間,患者每天上午8:00服藥,護士每天下午16:00為患者測量腋下體溫記錄如下:
.某位患者因患肺炎發熱,于12日至26日住院治療.醫生根據病情變化,從14日開始,以3天為一個療程,分別用三種不同的抗生素為該患者進行消炎退熱.住院期間,患者每天上午8:00服藥,護士每天下午16:00為患者測量腋下體溫記錄如下:
抗生素使用情況 | 沒有使用 | 使用“抗生素A”療 | 使用“抗生素B”治療 | |||||
日期 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 |
體溫( | 38.7 | 39.4 | 39.7 | 40.1 | 39.9 | 39.2 | 38.9 | 39.0 |
抗生素使用情況 | 使用“抗生素C”治療 | 沒有使用 | |||||
日期 | 20日 | 21日 | 22日 | 23日 | 24日 | 25日 | 26日 |
體溫( | 38.4 | 38.0 | 37.6 | 37.1 | 36.8 | 36.6 | 36.3 |
(I)請你計算住院期間該患者體溫不低于![]() 的各天體溫平均值;
的各天體溫平均值;
(II)在19日—23日期間,醫生會隨機選取3天在測量體溫的同時為該患者進行某一特殊項目“a項目”的檢查,記X為高熱體溫下做“a項目”檢查的天數,試求X的分布列與數學期望;
(III)抗生素治療一般在服藥后2-8個小時就能出現血液濃度的高峰,開始殺滅細菌,達到消炎退熱效果.假設三種抗生素治療效果相互獨立,請依據表中數據,判斷哪種抗生素治療效果最佳,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (其中
(其中![]() 為參數),以原點
為參數),以原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸建立極坐標系,曲線
軸非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設點![]() ,
,![]() 分別是曲線
分別是曲線![]() ,
,![]() 上兩動點且
上兩動點且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知
中,已知![]() 是曲線
是曲線![]() (
(![]() 為參數)上的動點,將
為參數)上的動點,將![]() 繞點
繞點![]() 順時針旋轉90°得到
順時針旋轉90°得到![]() ,設點
,設點![]() 的軌跡為曲線
的軌跡為曲線![]() .以坐標原點
.以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在極坐標系中,直線![]() 與曲線
與曲線![]() 分別相交于異于極點
分別相交于異于極點![]() 的
的![]() 兩點,點
兩點,點![]() ,當
,當![]() 時,求直線
時,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com