
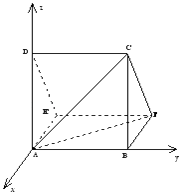
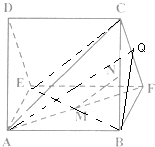
【題目】一個多面體的直觀圖(圖1)及三視圖(圖2)如圖所示,其中M,N分別是AF,BC的中點 
(1)求證:MN∥平面CDEF:
(2)求二面角A﹣CF﹣B的余弦值;
【答案】
(1)證明:由三視圖知,
該多面體是底面為直角三角形的直三棱柱ADE﹣BCF,
且AB=BC=BF=4,DE=CF= ![]() ,∠CBF=90°,
,∠CBF=90°,
連結BE,M在BE上,連結CE
EM=BM,CN=BN,所以MN∥CE,CE面CDEF,
所以MN∥平面CDEF.
(2)解法一:作BQ⊥CF于Q,連結AQ,
面BFC⊥面ABFE,面ABFE∩面BFC=BF,
AB面ABFE,AB⊥BF,
∴AB⊥面BCF,
CF面BCF,∴AB⊥CF,BQ⊥CF,AB∩BQ=B,
∴CF⊥面ABQ,AQ面ABQ,
AQ⊥CF,∴∠AQB為所求的二面角的平面角,
在Rt△ABQ中,tan∠AQB= ![]() =
= ![]() =
= ![]() ,
,
∴cos ![]() ,
,
∴二面角A﹣CF﹣B的余弦值為 ![]() .
.
解法二:以EA,AB,AD所在直線為x軸,y軸,z軸,
建立空間直角坐標系,
A(0,0,0),B(0,4,0),C(0,4,4),F(﹣4,4,0),
面CBF法向量為 ![]() ,
,
![]() ,
,
設面ACF法向量為 ![]() ,
,
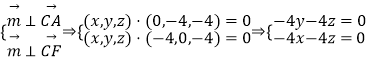
取z=﹣1,所以 ![]()
設二面角為θ,
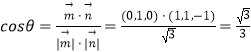 ,
,
∴二面角A﹣CF﹣B的余弦值為 ![]() .
.
【解析】(Ⅰ)由三視圖知,該多面體是底面為直角三角形的直三棱柱ADE﹣BCF,且AB=BC=BF=4,DE=CF= ![]() ,∠CBF=90°,由此能證明MN∥平面CDEF.(Ⅱ)(法一)作BQ⊥CF于Q,連結AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB為所求的二面角的平面角,由此能求出二面角A﹣CF﹣B的余弦值.(Ⅱ)(法二):以EA,AB,AD所在直線為x軸,y軸,z軸,建立空間直角坐標系,利用向量法能求出二面角A﹣CF﹣B的余弦值.
,∠CBF=90°,由此能證明MN∥平面CDEF.(Ⅱ)(法一)作BQ⊥CF于Q,連結AQ,由已知得AB⊥面BCF,AB⊥CF,BQ⊥CF,∠AQB為所求的二面角的平面角,由此能求出二面角A﹣CF﹣B的余弦值.(Ⅱ)(法二):以EA,AB,AD所在直線為x軸,y軸,z軸,建立空間直角坐標系,利用向量法能求出二面角A﹣CF﹣B的余弦值.
【考點精析】解答此題的關鍵在于理解直線與平面平行的判定的相關知識,掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行.


科目:高中數學 來源: 題型:
【題目】如圖,在邊長為4的菱形![]() 中,
中, ![]() ,點
,點![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 上.點
上.點![]() 與點
與點![]() 、
、![]() 不重合,
不重合, ![]() ,
, ![]() ,沿
,沿![]() 將
將![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)記三棱錐![]() 的體積為
的體積為![]() ,四棱錐
,四棱錐![]() 的體積為
的體積為![]() ,且
,且![]() ,求此時線段
,求此時線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A,B,C所對的邊分別為a,b,c,向量 ![]() =(c+a,b),
=(c+a,b), ![]() =(c﹣a,b﹣c),且
=(c﹣a,b﹣c),且 ![]() ⊥
⊥ ![]() .
.
(1)求角A的大小;
(2)若a=3,求△ABC周長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,OA、OB是兩條公路(近似看成兩條直線), ![]() ,在∠AOB內有一紀念塔P(大小忽略不計),已知P到直線OA、OB的距離分別為PD、PE,PD=6千米,PE=12千米.現經過紀念塔P修建一條直線型小路,與兩條公路OA、OB分別交于點M、N.
,在∠AOB內有一紀念塔P(大小忽略不計),已知P到直線OA、OB的距離分別為PD、PE,PD=6千米,PE=12千米.現經過紀念塔P修建一條直線型小路,與兩條公路OA、OB分別交于點M、N. 
(1)求紀念塔P到兩條公路交點O處的距離;
(2)若紀念塔P為小路MN的中點,求小路MN的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果不等式ax2+bx+c>0的解集為{x|﹣2<x<4},那么對于函數f(x)=ax2+bx+c應有( )
A.f(5)<f(2)<f(﹣1)
B.f(﹣1)<f(5)<f(2)
C.f(2)<f(﹣1)<f(5)
D.f(5)<f(﹣1)<f(2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場在一部向下運行的手扶電梯終點的正上方豎直懸掛一幅廣告畫.如圖,該電梯的高AB為4米,它所占水平地面的長AC為8米.該廣告畫最高點E到地面的距離為10.5米.最低點D到地面的距離6.5米.假設某人的眼睛到腳底的距離MN為1.5米,他豎直站在此電梯上觀看DE的視角為θ. 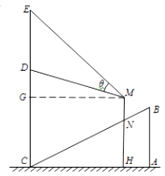
(1)設此人到直線EC的距離為x米,試用x表示點M到地面的距離;
(2)此人到直線EC的距離為多少米,視角θ最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為6,點E,F分別在邊AB,AD上,AE=AF=4,現將△AEF沿線段EF折起到△A′EF位置,使得A′C=2 ![]() .
. 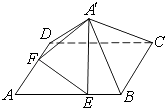
(1)求五棱錐A′﹣BCDFE的體積;
(2)求平面A′EF與平面A′BC的夾角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
某港灣的平面示意圖如圖所示, ![]() ,
, ![]() ,
, ![]() 分別是海岸線
分別是海岸線![]() 上的三個集鎮,
上的三個集鎮, ![]() 位于
位于![]() 的正南方向6km處,
的正南方向6km處, ![]() 位于
位于![]() 的北偏東
的北偏東![]() 方向10km處.
方向10km處.
(Ⅰ)求集鎮![]() ,
, ![]() 間的距離;
間的距離;
(Ⅱ)隨著經濟的發展,為緩解集鎮![]() 的交通壓力,擬在海岸線
的交通壓力,擬在海岸線![]() 上分別修建碼頭
上分別修建碼頭![]() ,開辟水上航線.勘測時發現:以
,開辟水上航線.勘測時發現:以![]() 為圓心,3km為半徑的扇形區域為淺水區,不適宜船只航行.請確定碼頭
為圓心,3km為半徑的扇形區域為淺水區,不適宜船只航行.請確定碼頭![]() 的位置,使得
的位置,使得![]() 之間的直線航線最短.
之間的直線航線最短.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com