
(本題8分)如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為正方形,
PA=AB=2,M, N分別為PA, BC的中點.
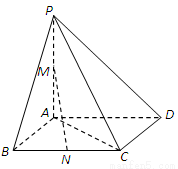
(Ⅰ)證明:MN∥平面PCD;
(Ⅱ)求MN與平面PAC所成角的正切值.
(Ⅰ)見解析;(Ⅱ)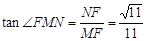 .
.
【解析】(I)取AD的中點E,連接NE,ME,易證: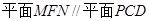 .
.
(II)找出(做)線面角是解題的關鍵.因為平面PAC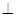 平面ABCD,所以過N作NF⊥AC于F,連接MF .所以NF⊥平面PAC, ∴∠FMN是MN與平面PAC所成的角.
平面ABCD,所以過N作NF⊥AC于F,連接MF .所以NF⊥平面PAC, ∴∠FMN是MN與平面PAC所成的角.
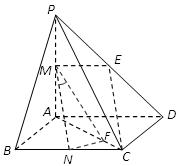
(Ⅰ)取PD的中點E,連接ME, CE.
∵M, N分別為PA, BC的中點,
∴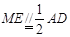 ,
,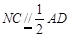 ,∴
,∴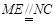 ,
,
∴MNCE是平行四邊形,∴MN∥CE,……………2分
∵CEÍ平面PCD,MNË平面PCD,
∴MN∥平面PCD.…………………………………2分
(Ⅱ)作NF⊥AC于F,連接MF.
∵PA⊥平面ABCD,∴PA⊥NF,又∵PA∩AC=A,
∴NF⊥平面PAC,∴∠FMN是MN與平面PAC所成的角.………2分
在Rt△MFN中,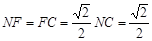 ,
,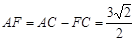 ,
,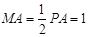 ,
,
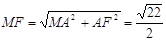 ,
,
∴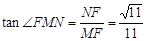 .……………………………………………2分
.……………………………………………2分


科目:高中數學 來源:2010年吉林省東北師大附中高一下學期期中考試數學 題型:解答題
(本題滿分8分)
如圖,在正方體 中,
中,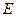 是
是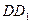 的中點,
的中點,
求證: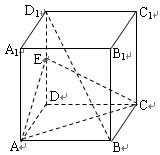
(1)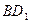 ∥平面
∥平面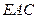 ;
;
(2)求異面直線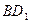 與
與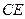 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源:浙江省臺州市09-10學年高一下學期期末質量評估數學試題 題型:解答題
(本題滿分8分)如圖,在底面是矩形的四棱錐
 中,
中, 底面
底面 ,
, 分
分
別是 的中點,求證:
的中點,求證:
(1) 平面
平面 ;
;
(2)平面 平面
平面 .高.考.資.源.網
.高.考.資.源.網
查看答案和解析>>
科目:高中數學 來源:2010年浙江省高二上學期10月月考數學卷 題型:解答題
(本題滿分8分)
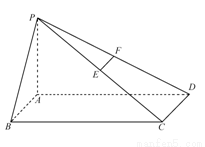
如圖,在四棱錐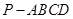 中,底面為直角梯形,
中,底面為直角梯形,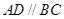 ,
, 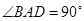 ,
,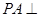 底面
底面 ,且
,且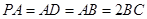 ,
,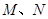 分別為
分別為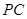 、
、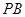 的中點。
的中點。
(Ⅰ)求證: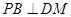 ;
;
(Ⅱ)求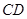 與平面
與平面 所成角的正弦值。
所成角的正弦值。

查看答案和解析>>
科目:高中數學 來源:2010年山東省北校區高二上學期第一次月考數學卷 題型:解答題
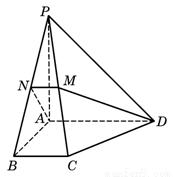
(本題滿分8分)如圖,在四棱錐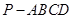 中,底面為直角梯形,
中,底面為直角梯形,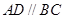 ,
,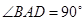 ,
,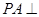 底面
底面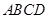 ,且
,且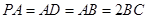 ,
,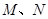 分別為
分別為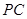 、
、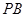 的中點。
的中點。
(Ⅰ)求證: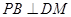 ;
;
(Ⅱ)求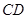 與平面
與平面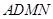 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com