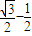若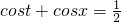 ,則函數(shù)y=cost-sin2x的值域是________.
,則函數(shù)y=cost-sin2x的值域是________.
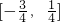
分析:由cost+cosx=

得cost=

-cosx,代入y=cost-sin
2x,配方后解決即可.
解答:∵cost+cosx=

,
∴cost=

-cosx①,
∴y=cost-sin
2x
=

-cosx-(1-cos
2x)
=cos
2x-cosx-

=
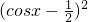
-

,
∵-1≤cost≤1,cost=

-cosx,
∴-1≤cosx-

≤1
∴-

≤cosx≤

,又-1≤cosx≤1,
∴-

≤cosx≤1.
∴當(dāng)cosx=-

,y
max=

,
當(dāng)cosx=

,y
min=-

.
故答案為:
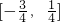
.
點評:本題考查復(fù)合三角函數(shù)的單調(diào)性,易錯點在于忽視cosx范圍的討論,屬于中檔題.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
若θ∈[-
,
],則函數(shù)y=cos(θ+
)+sin2θ的最小值是( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
若
-≤x≤,則函數(shù)
y=cos(x+)cos(x-)的值域為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
若
-≤X≤則函數(shù)
y=cos(x+)-cos(x-)的值域為
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:
題型:
若2α+β=π,則函數(shù)y=cosβ-6sinα的最大值和最小值為( )
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2010年高三數(shù)學(xué)綜合檢測試卷3(必修4)(解析版)
題型:選擇題
若θ∈[-
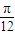
,

],則函數(shù)y=cos(θ+

)+sin2θ的最小值是( )
A.0
B.1
C.

D.
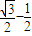
查看答案和解析>>

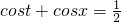 ,則函數(shù)y=cost-sin2x的值域是________.
,則函數(shù)y=cost-sin2x的值域是________. 名校通行證有效作業(yè)系列答案
名校通行證有效作業(yè)系列答案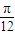 ,
, ],則函數(shù)y=cos(θ+
],則函數(shù)y=cos(θ+ )+sin2θ的最小值是( )
)+sin2θ的最小值是( )