
【題目】已知函數f(x)是正比例函數,函數g(x)是反比例函數,且f(1)=1,g(1)=2.
(1)求函數f(x)和g(x);
(2)判斷函數f(x)+g(x)的奇偶性;
(3)求函數f(x)+g(x)在(0,![]() ]上的最小值.
]上的最小值.
【答案】(1)![]() ;(2)函數f(x)+g(x)是奇函數;(3)
;(2)函數f(x)+g(x)是奇函數;(3)![]()
【解析】本試題主要是考查了函數的奇偶性和函數的解析式以及函數的最值的綜合運用。
(1)設f(x)=k1x,g(x)=![]() ,其中k1k2≠0然后結合已知中點的坐標的,餓到結論。
,其中k1k2≠0然后結合已知中點的坐標的,餓到結論。
(2)設h(x)=f(x)+g(x),則h(x)=x+![]() ,
,
∴函數h(x)的定義域是(-∞,0)∪(0,+∞).
∵h(-x)=-x+![]() =-(x+
=-(x+![]() )=-h(x)得到證明。
)=-h(x)得到證明。
(3)由(2)知h(x)=x+![]() ,設x1,x2是(0,
,設x1,x2是(0,![]() ]上的任意兩個實數,且x1<x2,,然后運用定義法得到單調性,確定最值。
]上的任意兩個實數,且x1<x2,,然后運用定義法得到單調性,確定最值。
解:(1)設f(x)=k1x,g(x)=![]() ,其中k1k2≠0.
,其中k1k2≠0.
∵f(1)=1,g(1)=2,∴k1×1=1,![]() =2.
=2.
∴k1=1,k2=2.∴f(x)=x,g(x)=![]() .
.
(2)設h(x)=f(x)+g(x),則h(x)=x+![]() ,
,
∴函數h(x)的定義域是(-∞,0)∪(0,+∞).
∵h(-x)=-x+![]() =-(x+
=-(x+![]() )=-h(x),
)=-h(x),
∴函數h(x)是奇函數,即函數f(x)+g(x)是奇函數.
(3)由(2)知h(x)=x+![]() ,設x1,x2是(0,
,設x1,x2是(0,![]() ]上的任意兩個實數,且x1<x2,
]上的任意兩個實數,且x1<x2,
則h(x1)-h(x2)=(x1+![]() )-(x2+
)-(x2+![]() )=(x1-x2)+(
)=(x1-x2)+(![]() -
-![]() )
)
=(x1-x2)(1-![]() )=
)=![]() ,
,
∵x1,x2∈(0,![]() ],且x1<x2,∴x1-x2<0,0<x1x2<2.
],且x1<x2,∴x1-x2<0,0<x1x2<2.
∴x1x2-2<0,(x1-x2)(x1x2-2)>0.
∴h(x1)>h(x2).
∴函數h(x)在(0,![]() ]上是減函數,函數h(x)在(0,
]上是減函數,函數h(x)在(0,![]() ]上的最小值是h(
]上的最小值是h(![]() )=2
)=2![]() .
.
即函數f(x)+g(x)在(0,![]() ]上的最小值是2
]上的最小值是2![]() .
.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x2-2aln x+(a-2)x,a∈R.
x2-2aln x+(a-2)x,a∈R.
(1)當a=1時,求函數f(x)的圖象在點(1,f(1))處的切線方程.
(2)是否存在實數a,對任意的x1,x2∈(0,+∞)且x1≠x2有![]() >a恒成立?若存在,求出a的取值范圍;若不存在,說明理由.
>a恒成立?若存在,求出a的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國個人所得稅法》規(guī)定,公民全月工資所得不超過3500元的部分不必納稅,超過3500元的部分為全月應納稅所得額,此項稅款按下表分段累計計算:

(1)某人10月份應交此項稅款為350元,則他10月份的工資收入是多少?
(2)假設某人的月收入為![]() 元,
元, ![]() ,記他應納稅為
,記他應納稅為![]() 元,求
元,求![]() 的函數解析式.
的函數解析式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人按下面的規(guī)則進行乒乓球比賽:第一局由甲、乙參加而丙輪空,以后每一局由前一局的獲勝者與
輪空者進行比賽,而前一局的失敗者輪空.比賽按這種規(guī)則一直進行到其中一人連勝兩局或打滿6局時停止.設在每局中參賽者勝負的概率均為![]() ,且各局勝負相互獨立,求:
,且各局勝負相互獨立,求:
(1)打滿3局比賽還未停止的概率;
(2)比賽停止時已打局數ξ的分布列與期望E(ξ).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班有兩個課外活動小組,其中第一小組有足球票6張,排球票4張;第二個小組有
足球票4張,排球票6張.甲從第一小組的10張票中任抽1張,乙從第二小組的10
張票中任抽1張.
(1)兩人都抽到足球票的概率是多少?
(2)兩人中至少有一人抽到足球票的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班為了提高學生學習英語的興趣,在班內舉行英語寫、說、唱綜合能力比賽,比賽分為預賽和決賽2個階段,預賽為筆試,決賽為說英語、唱英語歌曲,將所有參加筆試的同學(成績得分為整數,滿分100分)進行統(tǒng)計,得到頻率分布直方圖,其中后三個矩形高度之比依次為4:2:1,落在![]() 的人數為12人.
的人數為12人.
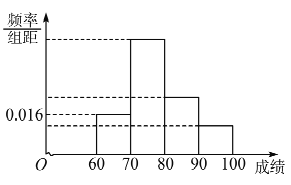
(Ⅰ)求此班級人數;
(Ⅱ)按規(guī)定預賽成績不低于90分的選手參加決賽,已知甲乙兩位選手已經取得決賽資格,參加決賽的選手按抽簽方式決定出場順序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)記甲乙二人排在前三位的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌手機銷售商今年1,2,3月份的銷售量分別是1萬部,1.2萬部,1.3萬部,為估計以后每個月的銷售量,以這三個月的銷售為依據,用一個函數模擬該品牌手機的銷售量y(單位:萬部)與月份x之間的關系,現(xiàn)從二次函數![]() 或函數
或函數![]() 中選用一個效果好的函數行模擬,如果4月份的銷售量為1.37萬件,則5月份的銷售量為__________萬件.
中選用一個效果好的函數行模擬,如果4月份的銷售量為1.37萬件,則5月份的銷售量為__________萬件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,且當
上的奇函數,且當![]() 時,
時, ![]() ;
;
(1)求函數![]() 在
在![]() 上的解析式并畫出函數
上的解析式并畫出函數![]() 的圖象(不要求列表描點,只要求畫出草圖)
的圖象(不要求列表描點,只要求畫出草圖)
(2)(ⅰ)寫出函數![]() 的單調遞增區(qū)間;
的單調遞增區(qū)間;
(ⅱ)若方程![]() 在
在![]() 上有兩個不同的實數根,求實數
上有兩個不同的實數根,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com