
【題目】已知函數![]() .
.
(1)求函數f(x)的最小正周期及單調遞增區間;
(2)求f(x)在區間![]() 上的最大值和最小值及相應的x值;
上的最大值和最小值及相應的x值;
【答案】(1)![]() ;[
;[![]() ,
,![]() ],k∈Z;(2)詳見解析
],k∈Z;(2)詳見解析
【解析】
(1)利用二倍角公式和輔助角公式化簡f(x)解析式,由正弦函數圖像的性質即可得函數周期和單調遞增區間.
(2)由正弦函數的性質可得f(x)最大值和最小值及相應的x值.
(1)∵f(x)=4sin3xcosx-2sinxcosx-![]() cos4x
cos4x
=sin2x×(1-cos2x)-sin2x-![]() cos4x
cos4x
=-![]() sin4x-
sin4x-![]() cos4x
cos4x
=-![]() sin(4x+
sin(4x+![]() ),
),
∴函數f(x)的最小正周期T=![]() .
.
∵由2kπ+![]() ≤4x+
≤4x+![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,可得:
,k∈Z,可得:![]() ,k∈Z,
,k∈Z,
∴函數f(x)的單調遞增區間為:[![]() ,
,![]() ],k∈Z;
],k∈Z;
(2)∵x∈[0,![]() ],
],
∴4x+![]() ,
,
∴sin(4x+![]() )∈[-
)∈[-![]() ,1],
,1],
∴f(x)=-![]() sin(4x+
sin(4x+![]() )∈[-
)∈[-![]() ,
,![]() ],
],
可得當x=![]() 時,f(x)在區間[0,
時,f(x)在區間[0,![]() ]上的最大值為
]上的最大值為![]() ,
,
當x=![]() 時,取得最小值為
時,取得最小值為![]() .
.


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】某重點中學100位學生在市統考中的理科綜合分數,以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.

(1)求直方圖中![]() 的值;
的值;
(2)求理科綜合分數的眾數和中位數;
(3)在理科綜合分數為![]() ,
, ![]() ,
, ![]() ,
, ![]() 的四組學生中,用分層抽樣的方法抽取11名學生,則理科綜合分數在
的四組學生中,用分層抽樣的方法抽取11名學生,則理科綜合分數在![]() 的學生中應抽取多少人?
的學生中應抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 滿足:①圓心在第一象限,截
滿足:①圓心在第一象限,截![]() 軸所得弦長為2;②被
軸所得弦長為2;②被![]() 軸分成兩段圓弧,其弧長的比為
軸分成兩段圓弧,其弧長的比為![]() ;③圓心到直線
;③圓心到直線![]() 的距離為
的距離為![]() .
.
(Ⅰ)求圓![]() 的方程;
的方程;
(Ⅱ)若點![]() 是直線
是直線![]() 上的動點,過點
上的動點,過點![]() 分別做圓
分別做圓![]() 的兩條切線,切點分別為
的兩條切線,切點分別為![]() ,
, ![]() ,求證:直線
,求證:直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,直線l的參數方程為 ![]() (t為參數),在以直角坐標系的原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρ=
(t為參數),在以直角坐標系的原點O為極點,x軸的正半軸為極軸的極坐標系中,曲線C的極坐標方程為ρ= ![]()
(1)求曲線C的直角坐標方程和直線l的普通方程;
(2)若直線l與曲線C相交于A,B兩點,求△AOB的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x),g(x)滿足關系g(x)=f(x)f(x+α),其中α是常數.
(1)設f(x)=cosx+sinx,![]() ,求g(x)的解析式;
,求g(x)的解析式;
(2)設計一個函數f(x)及一個α的值,使得![]() ;
;
(3)當f(x)=|sinx|+cosx,![]() 時,存在x1,x2∈R,對任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
時,存在x1,x2∈R,對任意x∈R,g(x1)≤g(x)≤g(x2)恒成立,求|x1-x2|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓 ![]() =1(a>b>0)的左焦點為F,過點F的直線交橢圓于A,B兩點.|AF|的最大值是M,|BF|的最小值是m,滿足Mm=
=1(a>b>0)的左焦點為F,過點F的直線交橢圓于A,B兩點.|AF|的最大值是M,|BF|的最小值是m,滿足Mm= ![]() a2 .
a2 . 
(1)求該橢圓的離心率;
(2)設線段AB的中點為G,AB的垂直平分線與x軸和y軸分別交于D,E兩點,O是坐標原點.記△GFD的面積為S1 , △OED的面積為S2 , 求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱臺ABC﹣DEF中,已知平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3,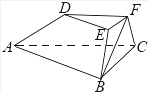
(1)求證:EF⊥平面ACFD;
(2)求二面角B﹣AD﹣F的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com