
 已知橢圓C:
已知橢圓C: 的長軸長是短軸長的
的長軸長是短軸長的 倍,F1,F2是它的左,右焦點.
倍,F1,F2是它的左,右焦點. ,|PF1|•|PF2|=4,求橢圓C的方程;
,|PF1|•|PF2|=4,求橢圓C的方程; |QM|,,求動點Q的軌跡方程.
|QM|,,求動點Q的軌跡方程.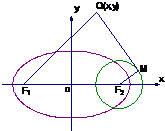 解:(1)依題意知
解:(1)依題意知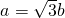 ①,
①,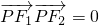 ,∴PF1⊥PF2,∴|PF1|2+|PF2|2=(2c)2=4(a2-b2)=8b2,
,∴PF1⊥PF2,∴|PF1|2+|PF2|2=(2c)2=4(a2-b2)=8b2, .
.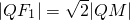 ,即|QF1|2=2|QM|2,
,即|QF1|2=2|QM|2,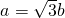 和|PF1|2+|PF2|2=(2c)2,以及|PF1|+|PF2|=2a 求出a2和b2的值,解得橢圓C的方程.
和|PF1|2+|PF2|2=(2c)2,以及|PF1|+|PF2|=2a 求出a2和b2的值,解得橢圓C的方程.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2010-2011學年黑龍江省哈爾濱市高三上學期期中考試文科數學卷 題型:解答題
(本小題滿分12分)
已知橢圓C: 的長軸長為4.
的長軸長為4.
(1)若以原點為圓心,橢圓短半軸長為半徑的圓與直線 相切,求橢圓焦點坐標;
相切,求橢圓焦點坐標;
(2)若點P是橢圓C上的任意一點,過原點的直線L與橢圓交于M,N兩點,直線PM,PN的斜率乘積為 ,求橢圓的方程.
,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年河北省衡水市冀州中學高二(下)6月月考數學試卷(理科)(解析版) 題型:解答題
 的長軸長為
的長軸長為 ,離心率
,離心率 .
. ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源:《第2章 圓錐曲線與方程》2010年單元測試卷(1)(解析版) 題型:解答題
 的長軸長為
的長軸長為 ,離心率
,離心率 .
. ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源:2011年安徽省淮南四中高考數學一模試卷(文科)(解析版) 題型:解答題
 的長軸長是短軸長的
的長軸長是短軸長的 倍,F1,F2是它的左,右焦點.
倍,F1,F2是它的左,右焦點. ,|PF1|•|PF2|=4,求橢圓C的方程;
,|PF1|•|PF2|=4,求橢圓C的方程; |QM|,,求動點Q的軌跡方程.
|QM|,,求動點Q的軌跡方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com