Question

設A（2，3，1），B（4，1，2），C（6，3，7），D（-5，-4，8），求D到平面ABC的距離．

Answer 1

【答案】分析：設平面ABC的法向量n=（x，y，z），利用待定系數法求出此法向量，最后結合點到平面的距離公式求解即得．
解答：解：設平面ABC的法向量n=（x，y，z），
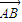
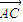
∵n•=0，n•=0，
∴
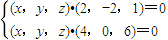
即
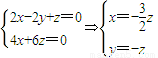
令z=-2，則n=（3，2，-2）．
∴cos＜n，＞=．
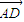
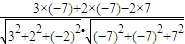
∴點D到平面ABC的距離為d，
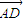
d=||•|cos＜n，＞|==．
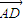
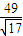
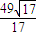
點評：本題主要考查了利用空間向量求點、線、面間的距離計算，考查運算能力和推理論證能力，屬于基礎題．