
【題目】在三棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .設D,E分別為PA,AC中點.
.設D,E分別為PA,AC中點.
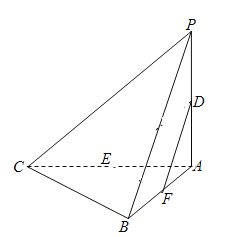
(Ⅰ)求證:![]() 平面PBC;
平面PBC;
(Ⅱ)求證:![]() 平面PAB;
平面PAB;
(Ⅲ)試問在線段AB上是否存在點F,使得過三點D,E,F的平面內的任一條直線都與平面PBC平行?若存在,指出點F的位置并證明;若不存在,請說明理由.
【答案】(Ⅰ)見證明;(Ⅱ)見證明;(Ⅲ)見解析.
【解析】
(Ⅰ)證明以DE∥平面PBC,只需證明DE∥PC;(Ⅱ)證明BC⊥平面PAB,根據線面垂直的判定定理,只需證明PA⊥BC,AB⊥BC;(Ⅲ)當點F是線段AB中點時,證明平面DEF∥平面PBC,可得平面DEF內的任一條直線都與平面PBC平行.
(Ⅰ)證明:因為點E是AC中點,點D為PA的中點,所以![]() .
.
又因為DE![]() 面PBC,PC面PBC,
面PBC,PC面PBC,
所以DE∥平面PBC.
(Ⅱ)證明:因為平面PAC⊥面ABC,平面PAC∩平面ABC=AC,又PA平面PAC,PA⊥AC,
所以PA⊥面ABC,
因為BC平面ABC,
所以PA⊥BC.
又因為AB⊥BC,且PA∩AB=A,
所以BC⊥面PAB.
(Ⅲ)
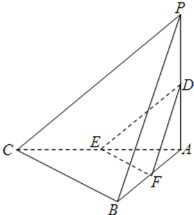
當點F是線段AB中點時,過點D,E,F的平面內的任一條直線都與平面PBC平行.
取AB中點F,連EF,連DF.
由(Ⅰ)可知DE∥平面PBC.
因為點E是AC中點,點F為AB的中點,
所以EF∥BC.
又因為EF![]() 平面PBC,BC平面PBC,
平面PBC,BC平面PBC,
所以EF∥平面PBC.
又因為DE∩EF=E,
所以平面DEF∥平面PBC,
所以平面DEF內的任一條直線都與平面PBC平行.
故當點F是線段AB中點時,過點D,E,F所在平面內的任一條直線都與平面PBC平行.


科目:高中數學 來源: 題型:
【題目】現采用隨機模擬的方法估計某運動員射擊4次,至少擊中3次的概率:先由計算器給出0到9之間取整數值的隨機數,指定0,1表示沒有擊中目標,2,3,4,5,6,7, 8,9表示擊中目標,以4個隨機數為一組,代表射擊4次的結果,經隨機模擬產生了 20組隨機數:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根據以上數據估計該射擊運動員射擊4次至少擊中3次的概率為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方形![]() 的邊長為1,點
的邊長為1,點![]() 在邊
在邊![]() 上,點
上,點![]() 在邊
在邊![]() 上,
上,![]() .動點
.動點![]() 從
從![]() 出發沿直線向
出發沿直線向![]() 運動,每當碰到正方形的邊時反彈,反彈時反射角等于入射角,當點
運動,每當碰到正方形的邊時反彈,反彈時反射角等于入射角,當點![]() 第一次碰到
第一次碰到![]() 時,
時,![]() 與正方形的邊碰撞的次數為( )
與正方形的邊碰撞的次數為( )
A. 4B. 3C. 8D. 6
查看答案和解析>>
科目:高中數學 來源: 題型:
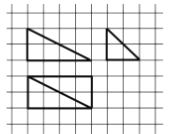
【題目】我國古代數學名著《九章算術·商功》中闡述:“斜解立方,得兩壍堵。斜解壍堵,其一為陽馬,一為鱉臑.陽馬居二,鱉臑居一,不易之率也.合兩鱉臑三而一,驗之以棊,其形露矣.”若稱為“陽馬”的某幾何體的三視圖如圖所示,圖中網格紙上小正方形的邊長為1,則對該幾何體描述:
①四個側面都是直角三角形;
②最長的側棱長為![]() ;
;
③四個側面中有三個側面是全等的直角三角形;
④外接球的表面積為![]() .
.
其中正確的個數為( )
A. 0B. 1
C. 2D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1為某省2018年1~4月快遞業務量統計圖,圖2是該省2018年1~4月快遞業務收入統計圖,下列對統計圖理解錯誤的是( )


A. 2018年1~4月的業務量,3月最高,2月最低,差值接近2000萬件
B. 2018年1~4月的業務量同比增長率均超過50%,在3月底最高
C. 從兩圖來看,2018年1~4月中的同一個月的快遞業務量與收入的同比增長率并不完全一致
D. 從1~4月來看,該省在2018年快遞業務收入同比增長率逐月增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點P與兩個定點O(0,0),A(3,0)的距離的比值為2,點P的軌跡為曲線C.
(1)求曲線C的軌跡方程
(2)過點(﹣1,0)作直線與曲線C交于A,B兩點,設點M坐標為(4,0),求△ABM面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為圓
為圓![]() 上一動點,圓心
上一動點,圓心![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,點
,點![]() 分別是線段
分別是線段![]() 上的點,且
上的點,且![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)直線![]() 與點
與點![]() 的軌跡
的軌跡![]() 只有一個公共點
只有一個公共點![]() ,且點
,且點![]() 在第二象限,過坐標原點
在第二象限,過坐標原點![]() 且與
且與![]() 垂直的直線
垂直的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,求
兩點,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com