
設關于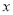 的方程
的方程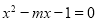 有兩個實根
有兩個實根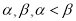 ,函數
,函數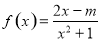 .
.
(1)求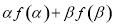 的值;
的值;
(2)判斷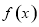 在區間
在區間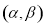 的單調性,并加以證明;
的單調性,并加以證明;
(3)若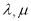 均為正實數,證明:
均為正實數,證明: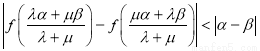
(1)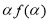 +
+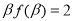 ;(2)單調遞增;(3)見解析.
;(2)單調遞增;(3)見解析.
【解析】
試題分析:(1)因為 是方程的
是方程的 的兩個實根,利用韋達定理即可得到
的兩個實根,利用韋達定理即可得到 的解析式,求出
的解析式,求出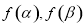 進而即可求出
進而即可求出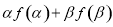 的值;(2)利用導數及二次函數的圖像來討論導數的正負,即可判斷函數的單調性;(3)首先求出
的值;(2)利用導數及二次函數的圖像來討論導數的正負,即可判斷函數的單調性;(3)首先求出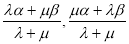 的取值范圍,然后根據函數的單調性判斷出函數值的取值范圍,把兩個函數值相減即可得到要證的結論.
的取值范圍,然后根據函數的單調性判斷出函數值的取值范圍,把兩個函數值相減即可得到要證的結論.
試題解析:(1)∵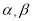 是方程
是方程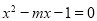 的兩個根, ∴
的兩個根, ∴ ,
,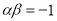 , 1分
, 1分
∴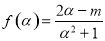 ,又
,又 ,∴
,∴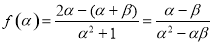
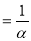 , 3分
, 3分
即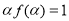 ,同理可得
,同理可得
∴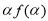 +
+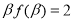 4分
4分
(2)∵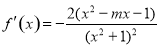 , 6分
, 6分
將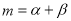 代入整理的
代入整理的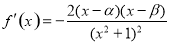 7分
7分
又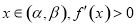 ,∴
,∴ 在區間
在區間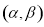 的單調遞增; 8分
的單調遞增; 8分
(3)∵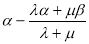
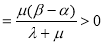 ,
,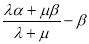
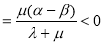
∴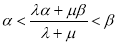 10分
10分
由(2)可知 ,同理
,同理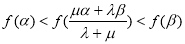
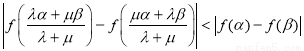 12分
12分
由(1)可知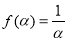 ,
,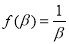 ,
,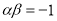 ,
,
∴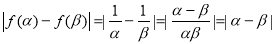
∴ 14分
14分
考點:函數與方程、函數的單調性、不等式的證明.


科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| OA |
| OB |
| α |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中數學 來源:人民教育出版社 代數 題型:
| |||||||||||||||
查看答案和解析>>
科目:高中數學 來源:2015屆山東省高三上學期11月檢測考試理科數學試卷(解析版) 題型:選擇題
各項都是正數的等比數列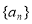 的公比
的公比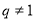 ,且
,且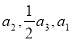 成等差數列,則
成等差數列,則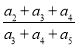 的值為( )
的值為( )
A. B.
B.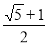 C.
C.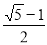 D.
D.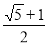 或
或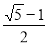
查看答案和解析>>
科目:高中數學 來源:2015屆山東省德州市高三10月月考理科數學試卷(解析版) 題型:解答題
已知函數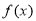 的定義域為
的定義域為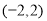 ,函數
,函數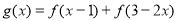
(1)求函數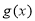 的定義域;
的定義域;
(2)若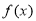 是奇函數,且在定義域上單調遞減,求不等式
是奇函數,且在定義域上單調遞減,求不等式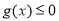 的解集.
的解集.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com